Juyeong Shin

KHU CSE 19
KHU DKE Lab.

4 분 소요

사고 실험보단 컴퓨터공학, 세상의 이치로 풀어써본 P, NP, NP-난해, NP-완전

P-NP 문제

  • 컴퓨터 과학, 수학계의 최종 보스인 밀레니엄 문제 중 하나
  • P 집합과 NP 집합이 같은지 다른지를 증명해야 하는 문제
  • P 집합은 이미(당연히) NP 집합의 부분집합
  • 반대로, 모든 NP 문제가 P 문제가 될 수 있다는 것까지 밝혀낸다면
  • NP 집합과 P 집합은 같은 것이다

Deterministic Turing Machine vs. Nondeterministic Turing Machine

Deterministic Turing Machine

  • 일반적으로 현대 사회에서 사용하는 컴퓨터의 근간이 되는 머신이다
  • Deterministic Finite State Machine으로 생각해 보자면..
    • 현재 상태에서 특정 입력(input)이 들어왔을 때,
    • 한 가지의 상태(Deterministic)로만 이동이 가능하다

DFA(Deterministic Finite Automaton)

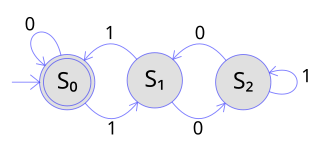
  • 위 그림에서 정점(vertex)은 상태, 간선(edge)은 input을 의미한다
  • 위 그림이 DFA인 이유는 하나의 정점에 대해 각 간선이 서로 다른 값을 가지기 때문이다
  • 즉, 현재 상태에서 주어진 input에 따라 이동 가능한 다른 상태는 오직 하나
  • 반대로, 현재 상태(정점)의 out-edge가 가진 값(input)이 유일(unique)하지 않다면, DFA가 아니다
    • 주어진 input에 대해 어느 간선을 선택할 것이며, 어느 정점으로 이동할 것인지 결정할 수가 없다!

Nondeterministic Turing Machine

  • 우리가 흔히 사용하는 컴퓨터의 형태는 아니다
  • 미래의 양자 컴퓨터는 가능할 수도..?
  • Nondeterministic Finite State Machine으로 생각해 보자면..
    • 현재 상태에서 특정 입력(input)이 들어왔을 때,
    • 여러 가지의 상태(Nondeterministic)로 이동이 가능하고
    • 동시에 여러 가지의 상태를 처리할 수 있다는 얘기이다!!

NFA(Nondeterministic Finite Automaton)

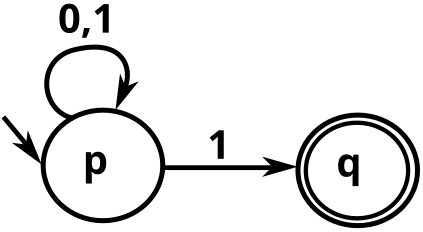
  • 위 그림에서, p state에서 1이라는 값을 가진 간선은 2개가 존재한다
  • 따라서, p state에서 1이라는 input에 대해 p state로 다시 이동할지, q state로 이동할지 결정할 수가 없다
  • 위와 같은 상태 머신을 NFA(Nondeterministic Finite Automaton)이라 한다

P 문제: Polynomial-time Problem

  • 결정론적 튜링 머신으로 다항 시간($O(N^k)$ Complexity) 내에 해(정답)를 도출할 수 있는 문제

NP 문제: Nondeterministic Polynomial-time Problem

  • 비결정론적 튜링 머신(양자 컴퓨터..?)으로 해(정답)을 다항 시간 내에 도출할 수 있음
  • 결정론적 튜링 머신(일반적인 컴퓨터)으로는 다항 시간 내에 해(정답)를 도출할 수 없음
  • NP 문제라 함은.. 결정론적 튜링 머신으로 문제를 해결하려 하면 $O(2^N)$ Time Complexity 이상이 소요된다

  • 검산(도출한 해가 맞는가?)은 다항 시간 내에 해결 가능하다

  • P 집합이 NP 집합의 부분집합인 이유는 너무나 자명하게도
    • Nondeterministic Turing Machine은 동시에 여러 상태를 처리할 수 있다

    • P 문제는 한 번에 한가지 상태만 처리해도 다항 시간 내에 문제를 해결할 수 있다

    • Nondeterministic Turing Machine에게 굳이 동시에 여러 문제를 처리하라 할 필요도 없이, 한번에 한가지 문제만 풀어내라 하여도
    • 어차피 다항 시간 내에 처리가 가능하다

NP-Hard: Nondeterministic Polynomial-time Hard

  • 적어도 NP 문제보다는 어려움
    • 어렵다는 뜻이 마냥 알고리즘이 이해하기 어렵다라는 뜻은 아니다..

  • 모든 NP 문제들을 문제 A로 다항 시간 내에 환원할 수 있다면, 문제 A는 NP-Hard 문제이다

  • 다항 시간 내에 환원 가능하다는 것은 무슨 뜻인가??
    • 예를 들어, 문제 A가 있고 문제 B가 있다고 하자
    • 문제 A는 덧셈 연산이다 (4 + 4)
    • 문제 B는 곱셈 연산이다 (4 * 4)
    • 문제 B(곱셈 연산)은 덧셈 연산을 3번 수행하는 문제(4 + 4 + 4 + 4)로 환원이 가능하다

    • 이때, 반복 횟수는 다항 횟수($T(N-1)$)번 수행하므로, 다항 시간 내로 환원가능한 것이다

    • 이때, 더 어려운 문제 A가 NP-Hard이다
      • 문제 B는 문제 A를 풀 수 있다면, 문제 A를 다항 횟수($O(N^k)$)번 반복하기만 하면 된다
      • 문제 A가 핵심 알고리즘(진짜 어려운 문제)이라면 문제 B는 응용 소프트웨어인 격
  • 물론, 덧셈 연산과 곱셈 연산은 다항 시간 내에 당연히 풀 수 있다
  • 환원이란 무엇인가에 대한 설명 정도로 남겨두자..
  • 덧셈이랑 곱셈 모두 P 문제임!!

NP-Complete: Nondeterministic Polynomial-time Complete

  • NP-Hard 중에는, Nondeterminstic Turing Machine으로 풀 수 없는 문제도 존재한다
    • 예를 들어, 주어진 NP 문제 A를 활용하는 NP 문제 B가 있다고 하자
    • 즉, 문제 B는 문제 A로 다항 시간 내에 환원이 가능하다
    • 그러나, 문제 A가 Nondeterministic Turing Machine으로도 풀 수 없는 문제라면

    • 문제 B도 풀 수 없다

    • 그럼에도, 여전히 문제 B는 문제 A로 다항 시간 내 환원은 가능하므로
    • 문제 A는 NP-Hard이고 풀 수도 없는 문제일 수 있다
    • 즉, 문제 A에 대한 정의는 가능하나, 해를 도출할 수 없는 경우이다
      • 대표적으로 엘런 튜링의 정지 문제(halting problem)가 있다
  • NP-Hard 중, Nondeterministic Turing Machine으로 풀 수 있으면 NP-Complete이다!!
    • 즉, NP-Hard 중에서, Nondeterministic Turing Machine으로 해를 구할 수 있으면 NP-Complete이다
    • 반대로, 다양한 NP 문제 중, 또 다른 NP 문제를 다항 횟수 내로 환원 가능하다면, 환원된 문제는 NP-Complete이다

P, NP, NP-Hard, NP-Complete

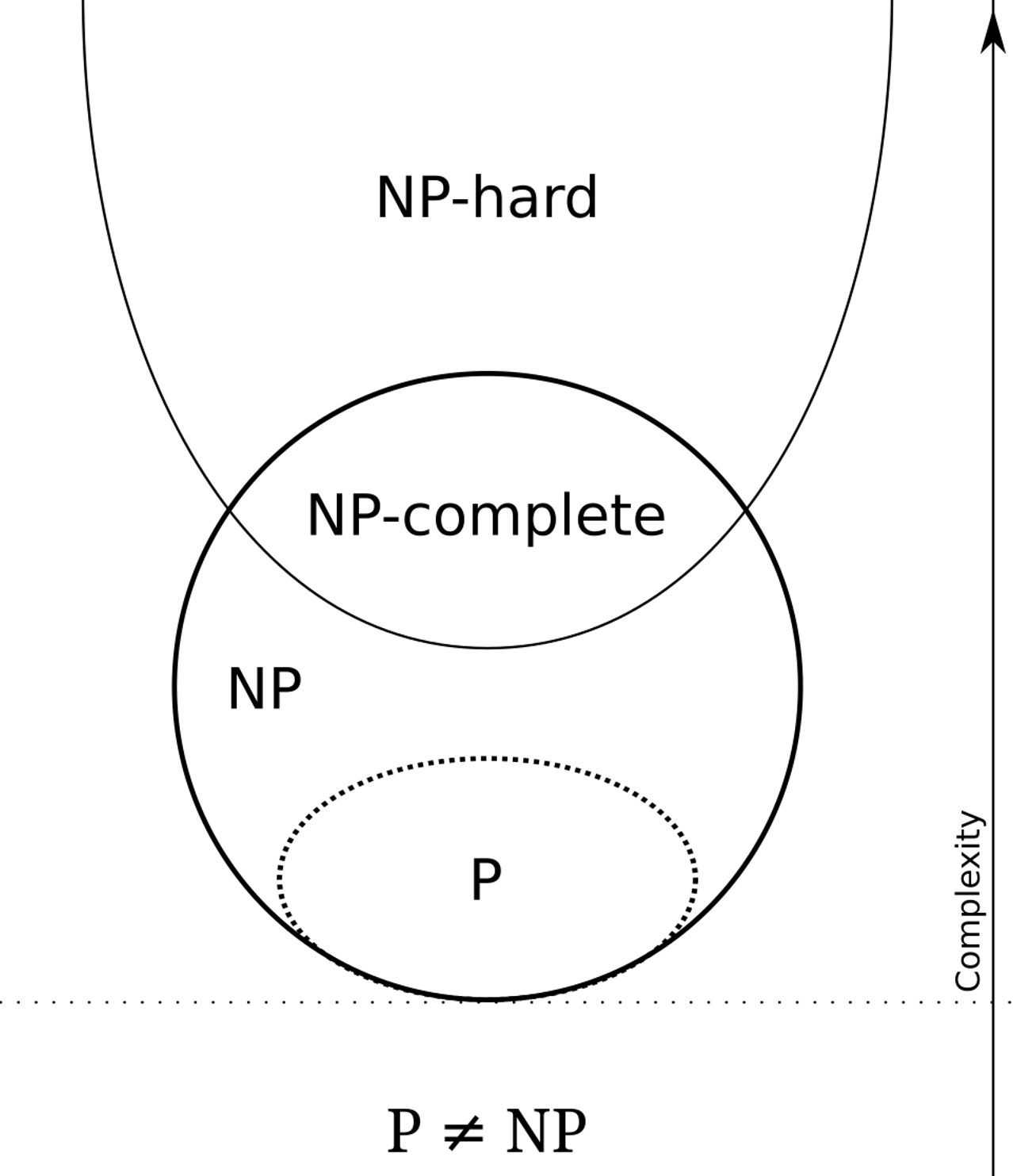
  • 세상에는 다양한 문제들이 존재할 것이다
    • 이러한 문제들을 정의할 수는 있을 것이고
    • 이를 전제 집합 $U$라 한다
  • 이러한 문제 중 일부는
    • 다항 시간 내에 해결이 가능한 문제도 존재하고 -> P 문제
    • 다항 시간 내에 해결하지는 못하나, 어쨌거나 해결은 가능한 문제가 존재하고 -> NP 문제
    • 다항 시간 내 해결하지 못하는 문제 중에서도, 핵심 알고리즘에 되는 문제가 존재할 것이다 -> NP-Complete
    • 그리고 어떠한 문제는 해가 존재하지 않을 수도 있다 -> NP-Complete을 제외한 NP-Hard
  • 마지막으로 P, NP, NP-Complete, NP-Hard라는 핵심 문제를 정의한 뒤 파생되는 다양한 응용 소프트웨어들이 존재할 것이다
    • 이는 전체 집합 $U$가 된다

P-NP 난제

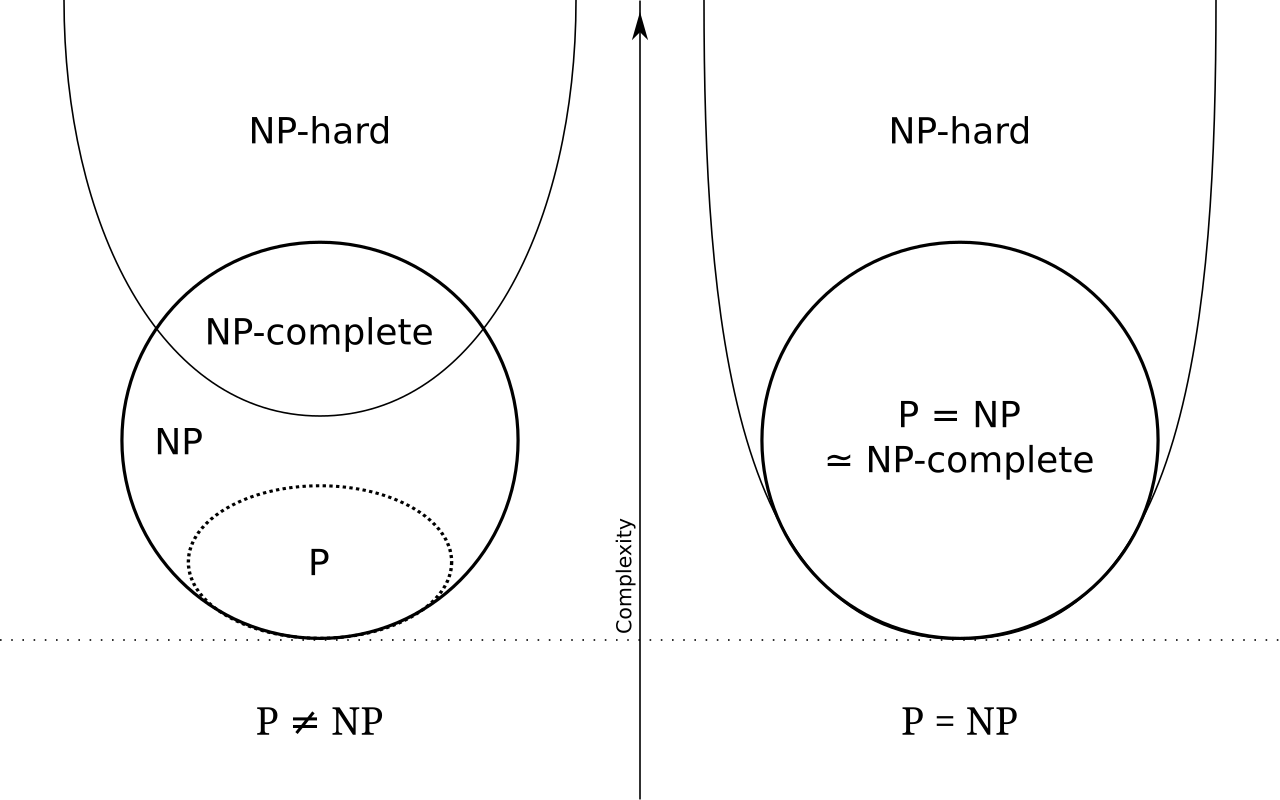
  • 모든 NP 문제를 P 문제로 환원 가능하다면
  • 지수 복잡도의 알고리즘을 다항 복잡도의 알고리즘으로 다항 시간 내 환원가능하다는 것이다
  • 즉, 지수 복잡도의 알고리즘을 다항 복잡도로 구현할 수 있다는 것!!
  • 아직 증명되지 않았다

마지막으로.. 알고리즘과 데이터마이닝

  • 결론적으로, NP-Hard(NP-난해)라 하면 난해하고 어렵고 복잡하고 시간이 많이 필요한 그런 문제를 일컫는다
  • 대용량 데이터에 대해서, NP-Hard 문제를 일반적인 컴퓨터로 무작정 풀어내려 시도하면.. 아마 내가 살아 있는 동안에는 해답을 보지 못할 것인데
  • 그런 복잡도의 문제를 근사해를 도출해서 구하는 다양한 알고리즘들이 제안되었으며
  • 그런 근사해를 구하는 방법을 제안하는 논문에서, 실제 해를 구하는 과정은 얼마나 복잡한지를 강조하기 위해서도
  • NP-Hard라는 단어를 자주 사용한다

참고 문헌

댓글남기기

참고