Randomized Quick Sort와 느낀 점

Randomized Quick Sort와 느낀 점

Quick Sort

• Quick Sort는 분할정복 알고리즘(Divide & Conquer)으로서, pivot을 잡고 partiton 함수로 pivot보다 작은 item들은 왼쪽에, pivot보다 큰 item들은 오른쪽에 분할한 뒤, 왼쪽 부분과 오른쪽 부분 각각을 재귀적으로 pivot을 잡고 partition하면서 정렬하는 알고리즘이다

• 우선 Quick Sort의 작동 방식을 살펴보자.

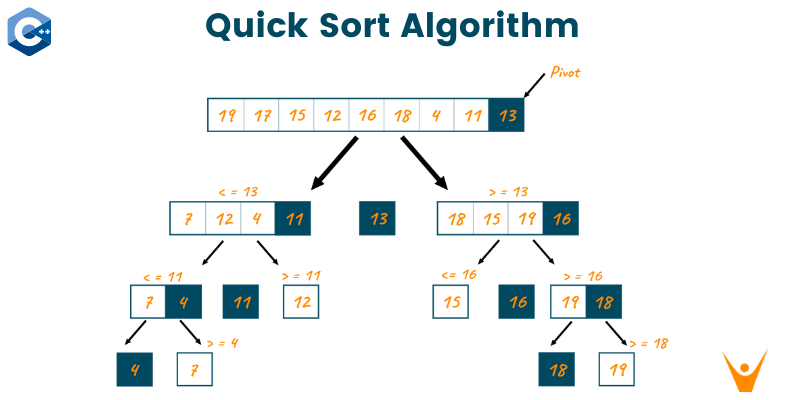
  1. pivot을 정한다(보통 left, right 중 하나를 사용한다)
  2. pivot을 기준으로 그보다 작은 아이템은 왼쪽에 배치하고 그보다 큰 아이템은 오른쪽에 배치한다
  3. 위 과정을 재귀적으로 반복한다
     • 종료 조건: left >= right
     • 즉, 연산할 배열의 크기가 1이거나 1보다 작은 경우

Quick Sort의 장점

• 평균 시간복잡도가 $O(N\log N)$로, 효율적인 정렬 알고리즘이다.

Quick Sort의 단점

• 최악의 경우, $O(N^2)$ 복잡도의 정렬알고리즘이다

• 어떤 상황에서 최악의 경우가 만들어지는가?

  • 배열이 내림차순으로 정렬되어 있다고 생각하자
  • 위 그림과 같이 pivot은 right로 설정하자
  • 그럼 pivot은 항상 제일 작은 값이 선택될 것이고 나머지 item들은 모두 pivot보다 크게 될 것이다
  • 현재 pivot으로 설정된 단 하나의 item만 제자리를 찾았고, 나머지는 상태 그대로 유지된다
    • 보통, $O(N\log N)$ 시간복잡도를 보장하는 heap sort, merge sort와 같은 경우 한번의 정렬 과정으로 나머지 item도 weak-ordering을 갖추게 된다
    • heap sort는 한번의 과정으로 나머지 item은 heap 규칙에 따른 weak-ordering이 수행되고
    • merge sort는 $\log N$을 구성하고 있는 각 계층에서 나눠진 배열 내에서의 ordering이 수행된다
  • 결론적으로, 배열 내 모든 item을 한 개씩 삽입하며 정렬을 수행하는 Exchange Sort와 같은 시간 복잡도를 가지게 된다.

Randomized Quick Sort란?

• 방금 얘기한 최악의 경우를 해결하기 위한 방법이다
• 되게 별거 없다. pivot을 랜덤으로 선택하면 된다
• N의 크기가 커질 수록 최악의 경우가 발생할 가능성은 0에 수렴할 것이다

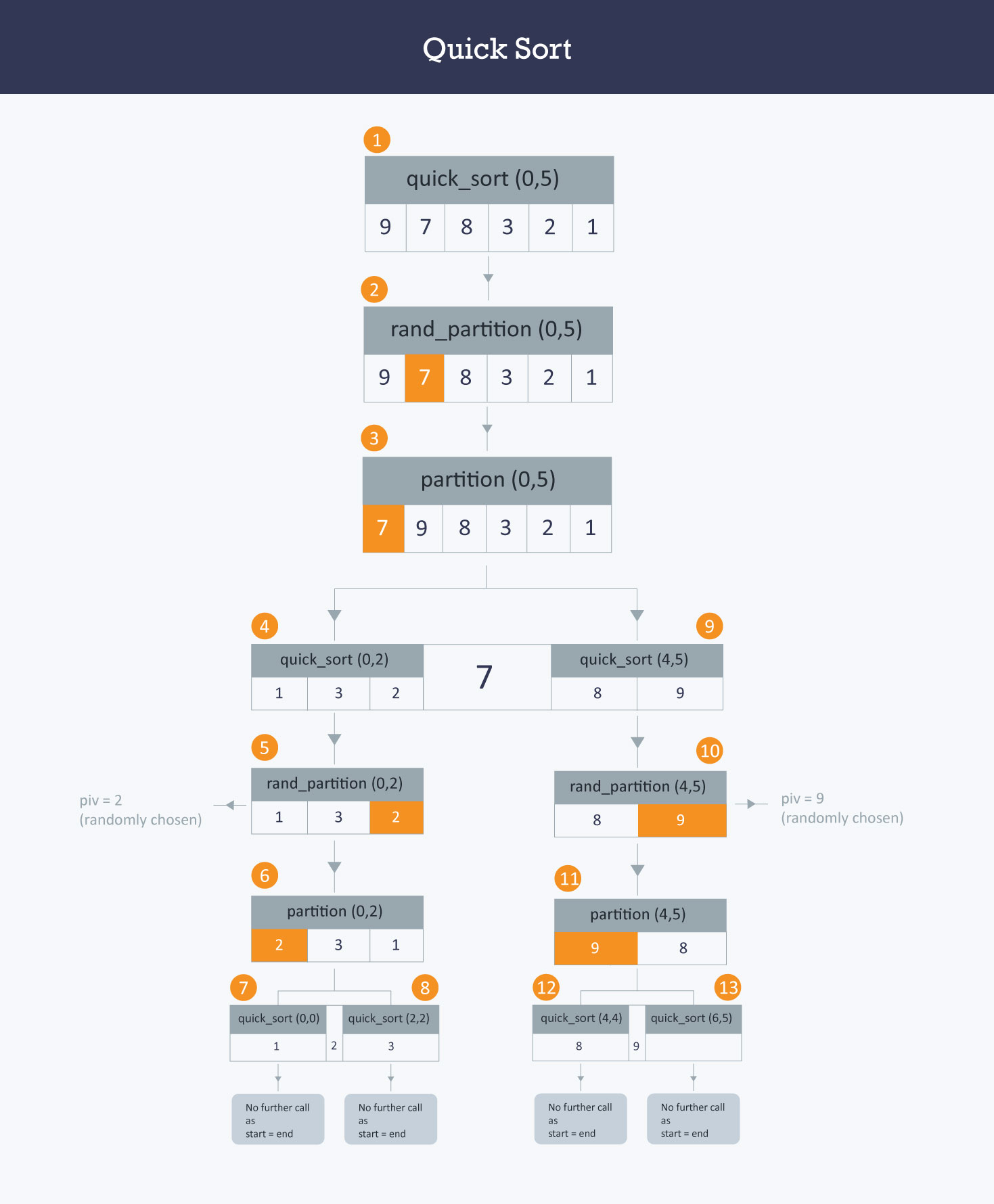
느낀점

quick sort(빠른 정렬)는 말로만 빠르지 되게 구리다고 생각했다. ‘item이 정렬된 상태일 상황(혹은 일부가 정렬된 상황)은 얼마든지 만들어질 수 있을 것 같은데, 저걸 어디에 써먹어?’라고 생각했기 때문이다.

그냥.. ‘왜 저정도의 생각조차 해보지 못했을까?’라는 생각이 들었다. 학교에서 배운 내용들을 이해하는데만 급급했다. 심지어 짧은 학식으로 ‘구린 알고리즘’이란 딱지를 내 머리 속에 붙여놓았었다. 더군다나 pivot을 하나로 고정한 것은 학생들의 편의를 봐준 것이지, 대부분의 라이브러리는 pivot을 무작위로 고르지 않는가?

그리고 저정도의 아이디어도 생각해보지 않고 ‘구린 알고리즘’이라는 딱지를 붙혀놓은 스스로가 부끄럽기도 했다.

태도를 고치자. 수업에서 배운 내용 착실하게 이해하고 암기하는 것도 물론 중요하다. 이게 1순위다. 하지만, 개선 방법과 아이디어를 고민해보는 습관을 더 들이고 싶었다.

참고 문헌

• Wikipedia. (2024.02.03). “퀵 정렬”. https://ko.wikipedia.org/wiki/퀵_정렬.
• Wikipedia. (2024.08.26). “힙 정렬”. https://ko.wikipedia.org/wiki/힙_정렬,
• Wikipedia. (2024.01.31). “합병 정렬”. https://ko.wikipedia.org/wiki/합병_정렬.
• favtutor. (2022.01.29). “Quick Sort in C++”. https://favtutor.com/blogs/quick-sort-cpp.
• hackerearth. “Quick Sort”. https://www.hackerearth.com/practice/algorithms/sorting/quick-sort/tutorial/.
• 오나기. (2019.01.09). “[알고리즘] 1. Randomized Quick Sort”. https://m.blog.naver.com/mycute0905/221437896729.
• 놀이터. (2019.04.21). “(Algorithm) Analysis of Randomized Quick Sort”. https://m.blog.naver.com/scy7351/221519210300.
• OpenAI. (2024). ChatGPT(Aug 8, 2024). GPT-4o. https://chat.openai.com.