[자료구조] Sorted List
Sorted List
List
- Linear relationship
- 리스트의 아이템들은 순서가 있음
- 첫번째 요소를 제외한 모든 아이템이 unique predecessor (유일한 앞선 아이템)을 가짐
- 모든 리스트는 길이를 가짐 (리스트 아이템의 갯수)

- Unsored List
- 아이템들이 정렬되지 않은 리스트
- Sorted List
- 아이템들이 정렬된 리스트
List에 필요한 Operators
- Constructor
- 리스트 객체를 생성하는데 필요한 생성자
- Transformer
- 리스트의 상태 (들어있는 아이템의 값, 리스트의 길이 등)을 변경
- Observer
- 리스트의 아이템이나 길이 등의 정보를 접근
- Iterator
- 리스트의 모든 아이템을 원하는 상태로 변경
- 리스트의 아이템에 순서대로 접근
Sorted List(Array Based)
- 리스트의 아이템들이 정렬된 상태로 배열됨
- 아이템들이 정렬되어 있으면, 탐색이 빈번하게 발생하는 경우 용이하게 사용할 수 있음
- 탐색 알고리즘: 이진 탐색(Binary Search)
- 삽입 Big-O: O(N)
- 아이템을 삽입할 위치로부터 기존 아이템을 모두 뒤로 미루어야 함
- 삭제 Big-O: O(N)
- 아이템을 삭제할 위치로부터 기존 아이템을 모두 앞으로 당겨야 함
- 탐색 Big-O: O(logN)
- 이진 탐색을 활용
이진 탐색(Binary Search)
- 정렬된 리스트의 중간 값과 찾고자 하는 값을 비교하여 탐색
Precondition
- 정렬된 리스트
이진 탐색의 동작 방식
- 배열의 중간 값을 가져옴
- 중간 값과 검색 값을 비교
- 중간 값이 검색 값과 같으면 종료 (mid == key)
- 중간 값보다 검색 값이 크면 기준 배열의 오른쪽 구간을 탐색 (mid < key)
- 중간 값보다 검색 값이 작으면 기준 배열의 왼쪽 구간을 탐색 (mid > key)
- 값을 찾거나 간격이 비어있을 때까지 반복
검색 예
- 배열의 가운데를 결정
mid = low + (high - low) / 2
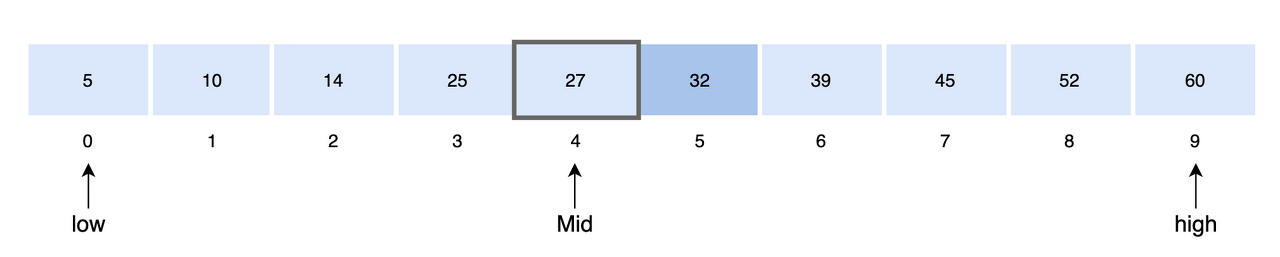
- 중앙 값과 검색 값을 비교
- A[4] < key 이므로 기존 구간의 오른쪽 구간이 탐색 범위
low = mid + 1
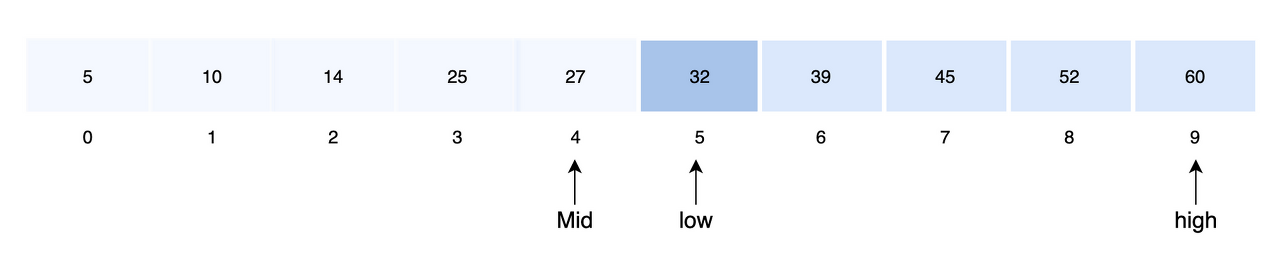
- 중앙 값을 결정
mid = low + (high - low) / 2
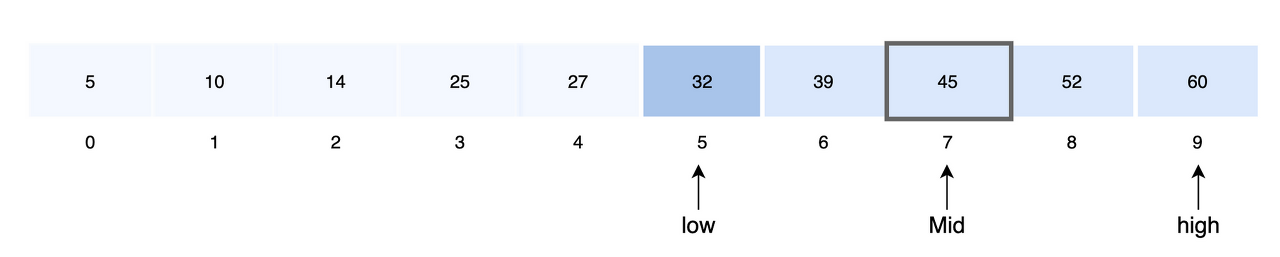
- 중앙 값과 검색 값을 비교
- A[7] < key 이므로 기존 구간의 왼쪽 구간이 탐색 범위
high = mid - 1
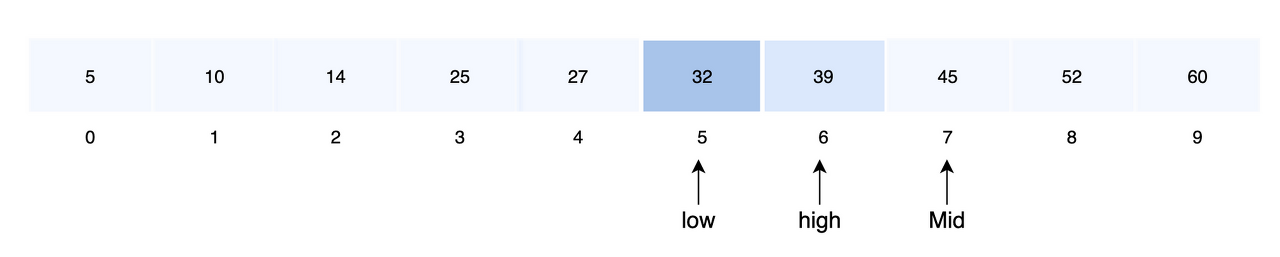
- 중앙 값을 결정
mid = low + (high - low) / 2
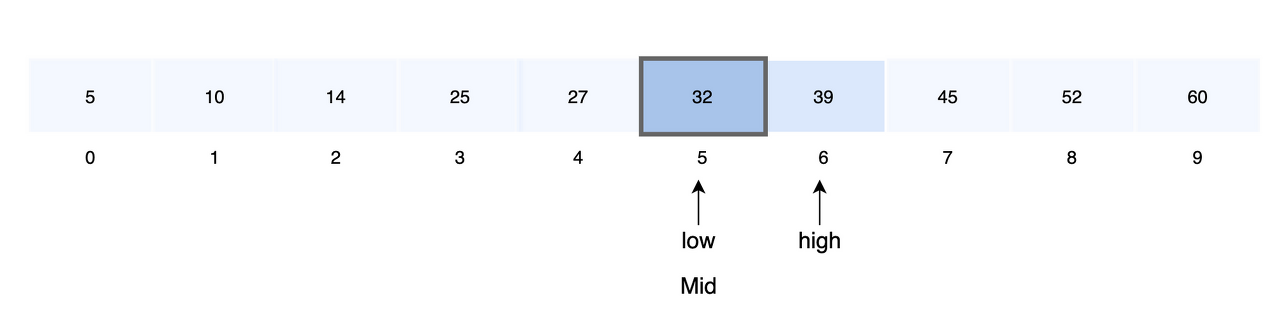
- 중앙 값과 검색 값을 비교
- A[5] = key 이므로 탐색을 종료
Sorted List Operators(Array Based)
- Transformers
- InsertItem
- DeleteItem
- MakeEmpty
- Observers
- RetrieveItem
- LengthIs
- IsFull
- Iterators
- ResetList
- GetNextItem
Source Code
Preprocessing
#include <iostream>
#include <climits>
#define MAX_ITEMS 50
using namespace std;
typedef int ItemType;
class SortedList;
Class Definition
class SortedList {
public:
SortedList();
[[nodiscard]] bool IsFull() const; // 리스트가 가득 차있는지 확인
[[nodiscard]] bool IsEmpty() const; // 리스트가 모두 비었는지 확인
[[nodiscard]] int LengthIs() const; // 리스트 길이 반환
[[nodiscard]] bool RetrieveItem(const ItemType& item) const; // 리스트에 파라미터로 준 아이템이 있는지 확인
void InsertItem(ItemType item); // 입력받은 아이템을 삽입
void DeleteItem(ItemType item); // 입력받은 아이템과 일치하는 아이템을 삭제
void MakeEmpty(); // 현재 리스트의 모든 요소 삭제
void ResetList(); // 아이템을 가리키는 CurrentPos를 0으로 초기화
ItemType GetNextItem(); // 다음 위치의 아이템을 반환
private:
int length; // 리스트의 길이 관리
ItemType info[MAX_ITEMS]{}; // 리스트에 저장된 데이터 관리
int currentPos; // 리스트의 현재 위치 관리
};
Class Constructor
SortedList::SortedList() {
length = 0;
currentPos = 0;
}
Class Transformer
void SortedList::InsertItem(const ItemType item) {
// array가 꽉 찬 경우 아이템 삽입 불가
if (IsFull()) {
cerr << "List is full. Cannot insert item." << endl;
return;
}
// 이진 탐색으로 삽입 위치 찾기
int first = 0, last = length - 1;
while (first <= last) {
int mid = (first + last) / 2;
if (info[mid] < item) {
first = mid + 1;
} else {
last = mid - 1;
}
}
const int correctPos = first; // 삽입 위치는 first가 최종적으로 가리키는 위치
// 삽입 위치 이후의 요소를 한 칸씩 뒤로 이동
for (int i = length; i > correctPos; i--) {
info[i] = info[i - 1];
}
// 삽입 위치에 아이템 삽입
info[correctPos] = item;
length++; // 리스트 길이 증가
}
void SortedList::DeleteItem(const ItemType item) {
// array가 비어있는 경우 아이템 삭제 불가
if (IsEmpty()) {
cerr << "List is empty. Cannot delete item." << endl;
return;
}
// 이진 탐색으로 삭제 위치 찾기
int first = 0, last = length - 1;
while (first <= last) {
int mid = (first + last) / 2;
if (info[mid] < item) {
first = mid + 1;
} else {
last = mid - 1;
}
}
const int correctPos = first; // 삭제 위치는 first가 최종적으로 가리키는 위치
// 해당 위치에 아이템을 한 칸씩 앞으로 이동
for (int i = correctPos; i < length; i++) {
info[i] = info[i+1];
}
length--; // 리스트 길이 감소
}
void SortedList::MakeEmpty() {
length = 0;
}
Class Observer
bool SortedList::RetrieveItem(const ItemType& item) const { // BinarySearch 구현
int first = 0; // 탐색 범위 시작 인덱스
int last = length - 1; // 탐색 범위 마지막 인덱스
bool found = false; // 탐색 완료 시 참으로 변경
while ((first <= last) && !found) {
const int midPoint = (first + last) / 2; // 탐색 범위 중심 계산
if (item < info[midPoint]) {
last = midPoint - 1;
}
else if (item > info[midPoint]) {
first = midPoint + 1;
}
else if (info[midPoint] == item) { // 일치하는 아이템이 있으면
found = true; // found 참으로 변환
}
}
return found;
}
int SortedList::LengthIs() const {
return length;
}
bool SortedList::IsFull() const {
return length == MAX_ITEMS;
}
bool SortedList::IsEmpty() const {
return length == 0;
}
Class Iterator
void SortedList::ResetList() {
currentPos = 0;
}
ItemType SortedList::GetNextItem() {
return info[currentPos++];
}
Main Function
int main() {
SortedList list;
list.InsertItem(30);
list.InsertItem(10);
list.InsertItem(20);
list.InsertItem(-7);
list.InsertItem(70);
list.InsertItem(60);
list.InsertItem(-5);
cout << "Length of list: " << list.LengthIs() << endl;
cout << "Items in the list (sorted): ";
list.ResetList();
for (int i = 0; i < list.LengthIs(); i++) {
cout << list.GetNextItem() << " ";
}
cout << endl;
if (list.IsFull())
cout << "The list is full." << endl;
else
cout << "The list is not full." << endl;
int item = 20;
list.ResetList();
if (list.RetrieveItem(item))
cout << "Item " << item << " found in the list." << endl;
else
cout << "Item " << item << " not found in the list." << endl;
list.DeleteItem(20);
cout << "Item 20 deleted." << endl;
cout << "Length of list after deletion: " << list.LengthIs() << endl;
cout << "Items in the list (sorted): ";
list.ResetList();
for (int i = 0; i < list.LengthIs(); i++) {
cout << list.GetNextItem() << " ";
}
cout << endl;
return EXIT_SUCCESS;
}
참고문헌
- Nell Dale. (2016). “C++ Plus Data Structues Sixth Edition”. Jones&Bartlett Learning.
- GeeksforGeeks. (2024). “ArrayList in Java”. https://www.geeksforgeeks.org/arraylist-in-java/.
- yoongrammer. (2024). “이진 탐색(Binary Search) 개념 및 구현”. https://yoongrammer.tistory.com/75.
- OpenAI. (2024). ChatGPT(Jan 10, 2024). GPT-4. https://chat.openai.com.
- meongju0o0. (2024). “sorted_list.cpp”. https://github.com/meongju0o0/meongju0o0-data-structure.


댓글남기기