Juyeong Shin

KHU CSE 19
KHU DKE Lab.

11 분 소요

BST(Binary Search Tree)와 KD트리 그리고 B트리와 R트리

트리를 이용한 인덱싱 기법들.. 근데 이제, 다차원을 곁들인

자료구조를 공부한 적이 있다면 BST(Binary Search Tree, 이진탐색트리)도 배웠을 것이다.

이진탐색트리는 상당히 매력적인 자료구조라 생각한다. BST를 사용하면 기존 Unsorted List의 O(N) Complexity를 O(logN) Complexity로 확연히 감소시켜준다.

하지만 문제가 있다. 기존 자료구조 교과서에서 BST를 다룰 때 어떻게 했었는가? BST 노드 하나 당 하나의 item만 삽입이 가능했다. 노드 하나 당 여러 item을 삽입시킨다 하여도 결국 정렬은 하나의 아이템을 기준으로 하거나 기껏해봐야 lexicographic order(사전식 순서)로만 정렬이 가능했다.

lexicographic order, 2개 속성일때 코드 예

bool cmp(const tuple<int, int>& a, const tuple<int, int>& b) {
    if(get<0>(a) != get<0>(b)) {
        return get<0>(a) < get<0>(b);
    }
    else {
        return get<1>(a) < get<1>(b);
    }
}


아래 테이블을 생각해보자. Name에 대해서는 정렬이 이루어져 있다. BST인지 아닌지를 떠나, 정렬이 되어 있는 상태에서는 이진탐색을 활용해 O(logN) Complexity로 탐색이 가능하니 Name에 대해서 ‘Eve’를 찾을 때는 O(logN) Complexity를 보장해준다.

하지만 Weight가 50kg인 사람을 찾고싶으면? 순차탐색이 최선이다. 즉, O(N) Complexity가 최선이라는 것이다.

ID Name Age Height Weight Country
1 Alice 25 165cm 55kg USA
2 Bob 30 180cm 80kg Canada
3 Charlie 35 175cm 70kg UK
4 David 28 170cm 68kg Australia
5 Eve 22 160cm 50kg Germany

이름에 대해 O(logN) Complexity를 보장해주면서 Weight에 대해서도 O(logN) Complexity를 보장해주고 싶으면 어떻게 해야할까?

앞으로 소개할 KD트리와 R트리는 이러한 한계점을 극복하기 위해 등장한 자료구조이다. 이들은 다차원 데이터를 효율적으로 탐색할 수 있게 해준다. 예를 들어 KD트리는 k차원 공간(k-Dimension)에서의 효율적인 탐색을 위한 구조로, 다양한 속성을 동시에 고려한 탐색이 가능하다.

BST, 결국 기본은 BST

BST란 무엇인가?

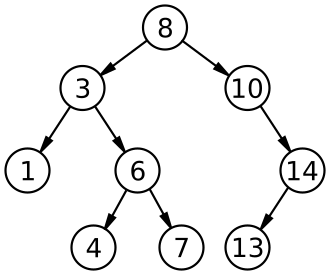
  • 이진탐색트리(BST, Binary Search Tree)는 아래와 같은 속성이 있는 이진트리 자료구조이다.
    • 각 노드에 값이 있다.
    • 값들은 전순서가 있다.(정렬이 가능하다.)
    • 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
    • 노드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이루어져 있다.
    • 좌우 하위 트리는 각각이 다시 이진탐색트리여야 한다.

BST에서 탐색은?

  • 위 그림을 예시로 보자. 아이템 ‘13’을 찾고자 하면 어떻게 해야할까?
  • 탐색하고자 하는 값을 루트 노드(최상위 노드, 예시에서 ‘8’)와 먼저 비교하고 일치할 경우 루트 노드를 반환
    • 불일치하고 탐색하고자 하는 값이 루트 노드의 값보다 작을 경우 왼쪽 서브 트리에서 재귀적으로 탐색
    • 불일치하고 탐색하고자 하는 값이 루트 노드의 값보다 큰 경우 오른쪽 서브 트리에서 재귀적으로 탐색
  • 위와같은 탐색 방식으로 O(logN) Time Complexity를 보장해줄 수 있다.

BST에서 삽입연산은 어떻게?

  • 삽입 전, 검색을 수행한다.
  • 트리를 검색한 후 키와 일치하는 노드가 없으면 마지막 노드에서 키와 노드의 크기를 비교하여 왼쪽이나 오른쪽 노드에 새로운 노드를 삽입한다.
    • 마지막 노드보다 큰 경우 말단 노드의 오른쪽에 새로운 노드 삽입
    • 마지막 노드보다 작은 경우 말단 노드의 왼쪽에 새로운 노드 삽입
      • 말단 노드(terminal node): 자식노드가 없는 노드(예시에서 ‘1’, ‘4’, ‘7’, ‘13’)
  • 삽입연산도 마찬가지로 O(logN) Time Complexity를 보장할 수 있다.

BST에서 삭제연산

  • 삭제하려는 노드의 자식 수에 따라
    • 자식 노드가 없는 노드(말단 노드) 삭제: 해당 노드를 단순히 삭제
    • 자식 노드가 1개인 노드 삭제: 해당 노드를 삭제하고 그 위치에 삭제된 노드의 서브트리를 대입
    • 자식 노드가 2개인 노드 삭제: 삭제하고자 하는 노드의 값을 해당 노드의 왼쪽 서브트리에서 가장 큰 값으로 변경하거나, 오른쪽 서브 트리에서 가장 작은 값으로 변경한 뒤, 해당 노드를 삭제
  • 삭제연산 또한 O(logN) Time complexity를 보장해준다.

한계점

  1. 항상 O(logN) Complexity를 보장해주지 않는다.
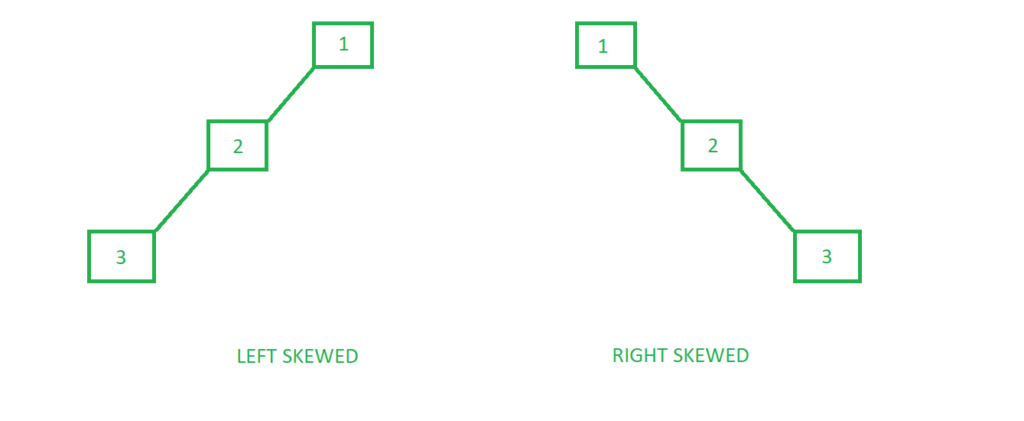
    • 극단적으로, skewed tree의 경우, O(N) Time Complexity가 되어버린다. skewed_tree
    • 이를 개선하기 위해, AVL트리나 Red-Black트리와 같은 자료구조도 존재한다.
  2. 다차원 속성에서는 적용이 불가능하다.
    • 이를 개선하기 위해 k-D트리와 같은 자료구조가 존재한다.

KD트리, BST를 다차원으로

KD트리(k-Dimensional tree)

  • 종류: 다차원 BST
  • 발명일: 1975

  • 발명자: 존 벤틀리

  • k차원 공간의 점들을 구조화하는 공간 분할 자료구조
  • 중심 데이터포인트를 기준으로 분할 초평면을 만들어 트리 생성
  • BST(Binary Search Tree)와 유사하나, k-Dimension 상의 데이터를 트리로 구축할 수 있음
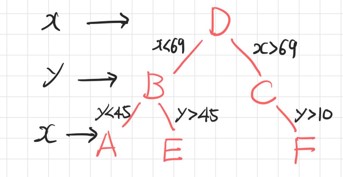
  • BST를 x축에 대해서 수행 -> y축에 대해서 수행 -> z축에 대해서 수행 -> x축에 대해서 수행 -> y축에 대해서 …

k-D Tree Construction Algorithm

  • Precondition
    • 2차원 실수 공간 (X측, Y축)
  1. X축에 대해 정렬한 후 중앙값을 기준으로 배열 분할
    • Y축에 대해 먼저 정렬하여 분할할 수도 있음
    • 이는 각 축의 분산에 의해 결정됨

  2. Y축에 대해 정렬한 후 중앙값을 기준으로 배열 분할

  3. 위 과정을 반복하면서 트리 생성

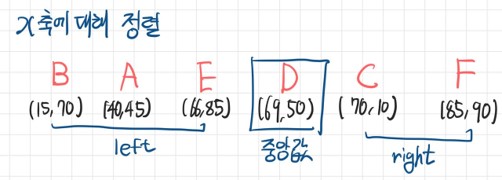
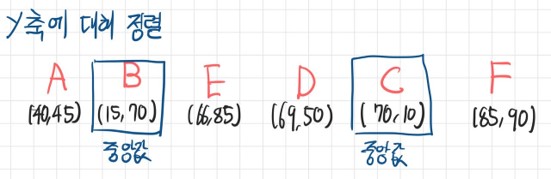
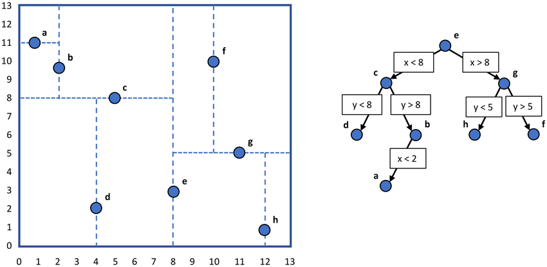
k-D Tree Nearest Neighbor Search Algorithm

  1. 새로운 점이 트리의 어디에 삽입되어야 하는지 탐색

  2. 도달한 리프 노드를 기준으로 자신이 속한 subtree를 우선적으로 탐색
    • 자신이 속한 subtree에서 k개의 최근접 이웃을 모두 탐색하지 못한 경우, 부모 노드의 subtree에서 순회

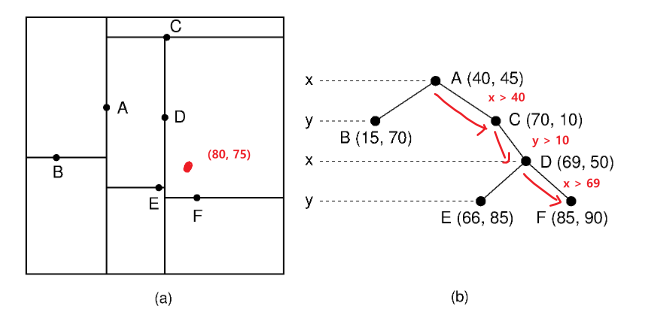
Time Complexity

  • Time Complexity(Notations)
    • Dimension: $D$
    • Number of Tuples: $N$
  • Time Complexity(Building)
    • 추가할 point가 어느 subtree에 위치하는지 탐색: $O(DlogN)$
    • 총 튜플 n개를 만족할 때가지 트리 구축: $O(N)$
    • 최종 Time Complexity: $O(DNlogN)$
  • Time Complexity(Search)
    • 평균적인 복잡도
      • 추가할 point가 어느 subtree에 위치하는지 탐색: $O(DlogN)$
    • 최악의 경우, i.e. Skewed Tree
      • 추가할 point가 어느 subtree에 위치하는지 탐색: $O(DN)$

B트리, 다시 1차원으로

B트리는 왜 필요할까?

B트리는 데이터베이스(mySQL, mongoDB, …)와 파일 시스템(NTFS, HFS+, …)에서 널리 사용되는 트리 자료구조 중 하나로 이진 트리를 확장해 하나의 노드가 가질 수 있는 자식노드의 최대 숫자가 2보다 큰 트리 구조이다.

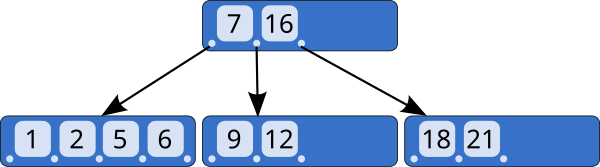
B트리는 삽입연산 시에 아직 삽입할 수 있는 자식노드가 남아 있는 경우 기존 트리 구조를 변경하지 않은 채로 추가적인 노드를 삽입할 수 있다. 마찬가지로, 삭제연산 시에도 트리 재균형 연산이 필요한 경우가 훨씬 줄어든다. 이러한 장점으로 데이터베이스나 파일 시스템에서 B트리 자료구조를 채택한다. 참고로 실제 구현은 B+트리로 작성되는 경우가 훨씬 빈번하다.

일반적으로 BST는 AVL트리, Red-Black트리와 같은 자가균형 이진트리로 구현되는데, 삽입, 삭제 연산시에 재균형 연산이 필요하다.

데이터베이스나 파일 시스템은 메모리보다 하드디스크를 더 중점적으로 관리해주는 소프트웨어이다. 이때, 하드디스크는 메모리에 비해 속도가 현저히 느리다. 이런 하드디스크 상에서 아이템 삽입, 삭제 시마다 트리 재균형 연산을 수행했다간 시스템의 속도가 무지하게 감소할 것이다. 반대로, 메모리를 저렇게 사용하는 것은 상당한 낭비이고 이러한 단점을 개선하기 위한 B*트리도 존재한다.

물론 B트리도 재균형 연산이 필요한 경우가 발생하지만, 재균형 연산이 필요한 경우가 BST에 비해 적고 더 효율적으로 재균형 연산을 수행할 수 있다. 이때, B트리의 차수(degree)가 클 수록 재균형 연산이 필요한 경우는 줄어들고 더 효율적인 재균형 연산이 가능하다.(트리의 높이가 낮아지기 때문)

B트리 노드 구조

  • 노드의 자식 수 제한: B트리의 각 노드는 최대 M개의 자식을 가질 수 있으며, 이를 차수(degree)라 한다. B트리의 차수 M이 주어지면:
    • 최대 M개의 자식 노드를 가질 수 있다.
    • 최대 M+1개의 키를 노드에 저장할 수 있다.
  • 균형 유지: 모든 리프 노드의 높이는 동일하며, 트리는 항상 균형 상태를 유지한다.
  • 키 배열: 각 노드의 키는 오름차순으로 정렬되며, 왼쪽 서브트리의 모든 키는 해당 키보다 작고, 오른쪽 서브트리의 모든 키는 그보다 크다.

B트리 탐색 연산

  • 탐색 연산은 이진 탐색과 유사하다. 각 노드에 있는 키들이 정렬되어 있으므로, 이진 탐색을 사용하여 원하는 키를 찾는다. 이때, 노드 내에서 탐색 시간복잡도는 O(logM)이다.
  • 탐색은 루트에서 시작해, 적절한 자식 노드로 이동하며 탐색을 반복한다. 트리의 높이는 O(logN)이므로, 탐색 연산의 총 시간복잡도는 O(logM * logN)이다.

B트리 삽입 연산

  1. 탐색: 삽입할 위치를 탐색한다. 삽입할 위치가 결정되면 해당 노드에 키를 삽입한다.
  2. 분할(Overflow): 노드에 이미 m+1개의 키가 있을 경우, 해당 노드는 더 이상 키를 추가할 수 없으므로 분할이 필요하다.
    • 중앙에 위치한 키를 부모 노드로 올리고, 나머지 키를 좌우 두 개의 새로운 자식 노드로 분할한다.
    • 부모 노드에 여유가 없을 경우, 부모 노드도 분할을 반복한다. 최악의 경우 루트 노드까지 분할이 일어나면서 트리의 높이가 1만큼 증가할 수 있다.

Case 1. 분할이 발생하지 않는 경우(M=3)

  • 말단 노드가 넘치지 않았다면, 오름차순으로 키를 삽입한다.

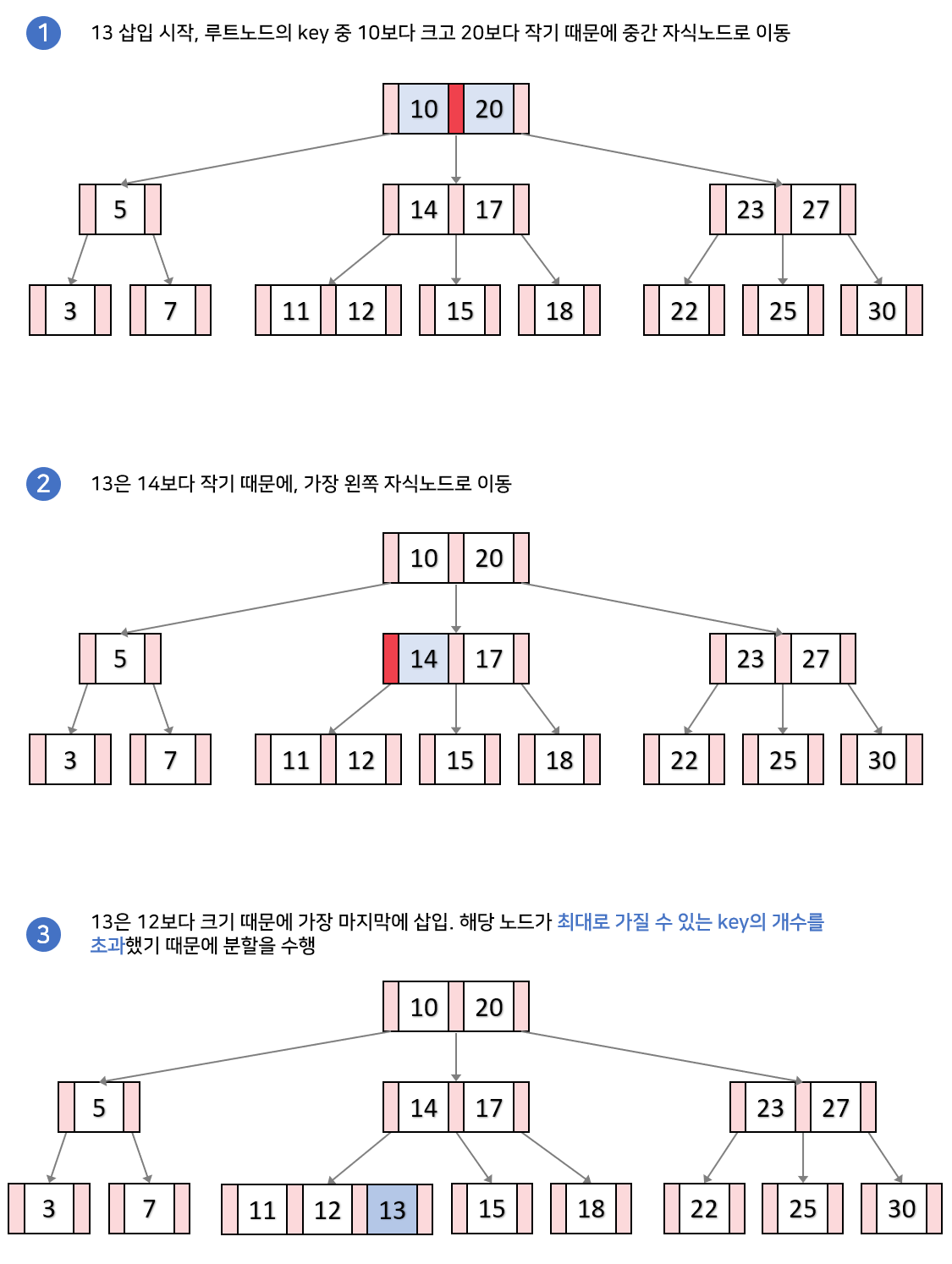
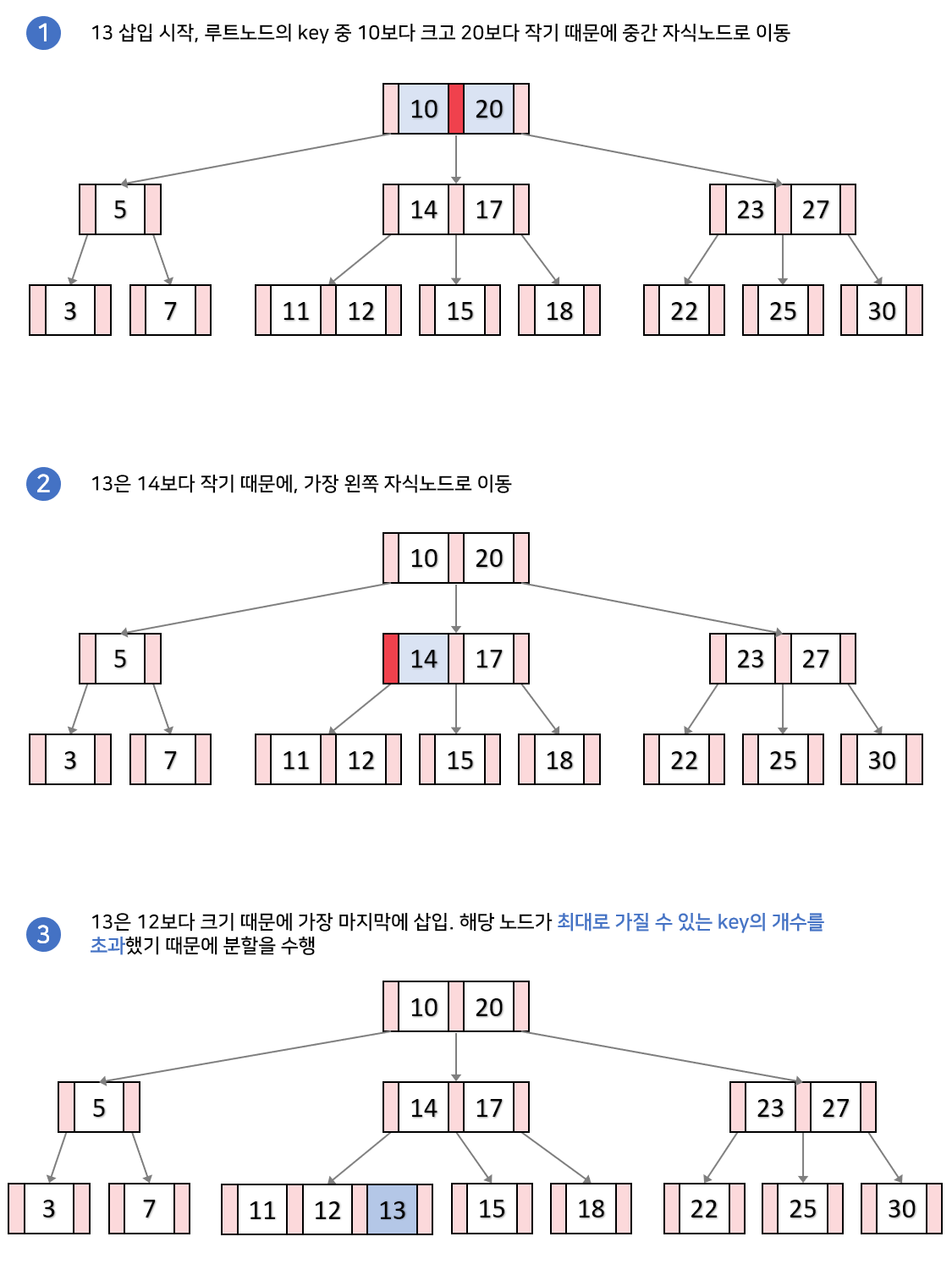
Case 2. 분할이 발생하는 경우(M=3)

  • 말단 노드에 키가 가득 찬 경우, 노드를 분할한다.
    • 노드가 넘치면 가운데 키(median key)를 기준으로 좌우 키를 분할하고 가운데 키는 승진한다.

B트리 삭제 연산

  1. 탐색: 삭제할 키를 먼저 탐색한다. 키가 리프 노드에 있을 경우, 바로 삭제한다.
  2. 재조정(Underflow): 삭제 후 노드에 너무 적은 키(최소 M/2 - 1개)가 남게 되면, 재조정이 필요하다. 이때 두 가지 방법이 사용된다:
    • 형제 노드로부터 차용(Borrow): 인접한 형제 노드에서 한 개의 키를 빌려와서 해당 노드의 키 개수를 채운다.
    • 병합(Merge): 만약 형제 노드에서 키를 빌릴 수 없다면, 해당 노드를 형제 노드와 병합하고, 부모 노드에서 키를 하나 내려준다. 이때, 부모 노드의 키가 부족하면 부모 노드도 병합 또는 차용 과정을 거친다. 이때, 이 과정이 루트 노드까지 올라가면 트리의 높이가 1만큼 줄어들 수 있다.

말단 노드에서 삭제

Case 1. 삭제하고 재조정이 필요하지 않는 경우(M=2)
  • 말단 노드에서 아이템을 삭제한다.

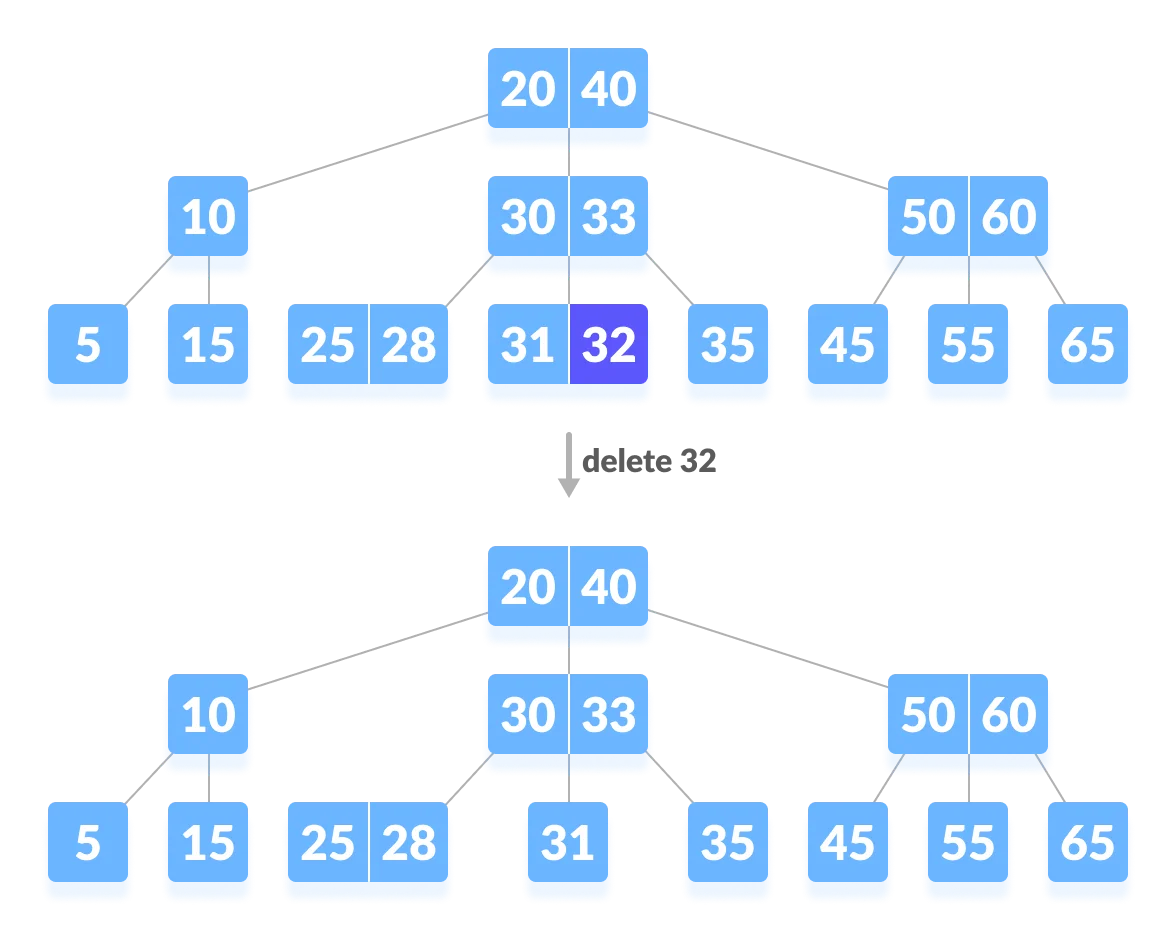
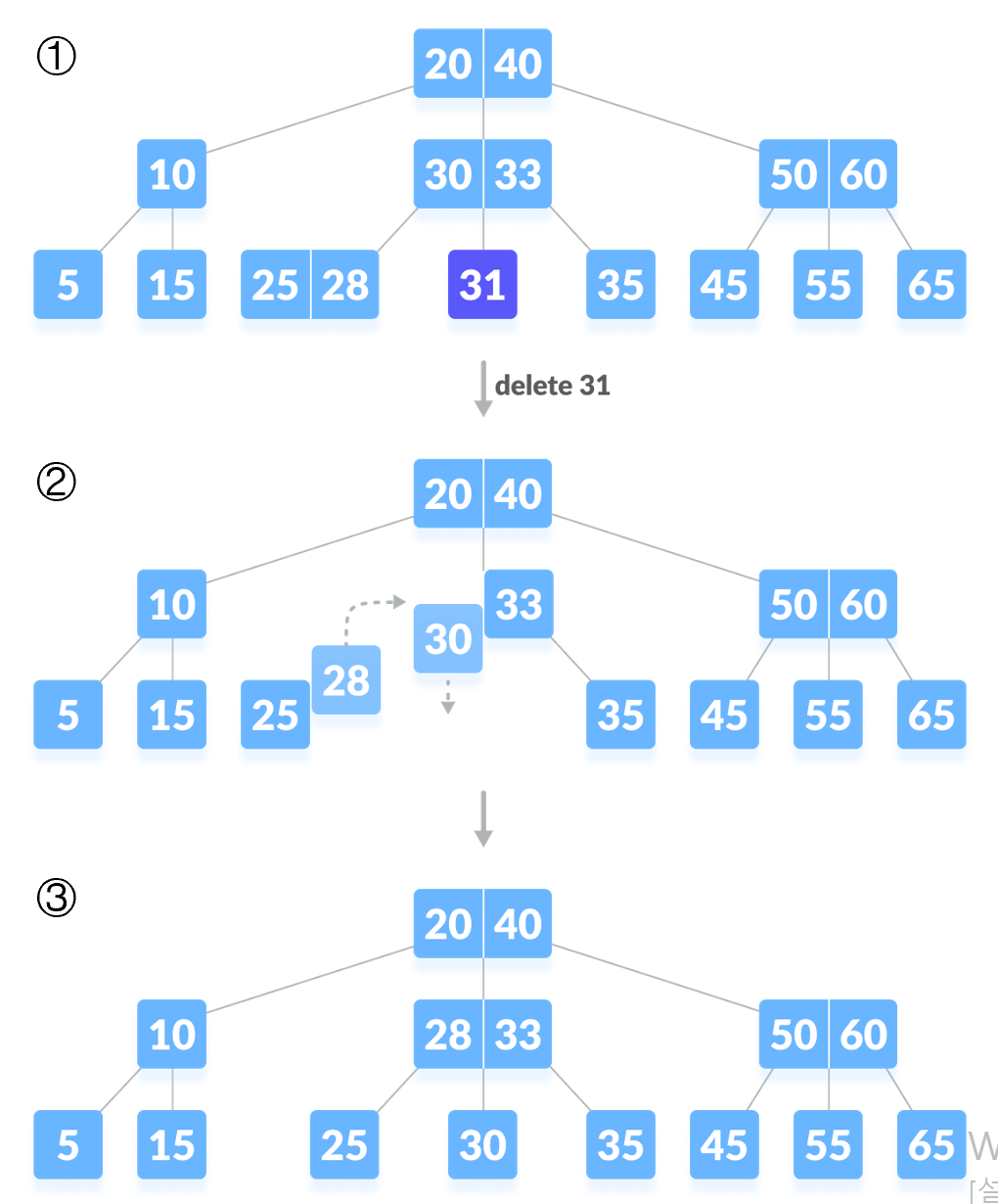
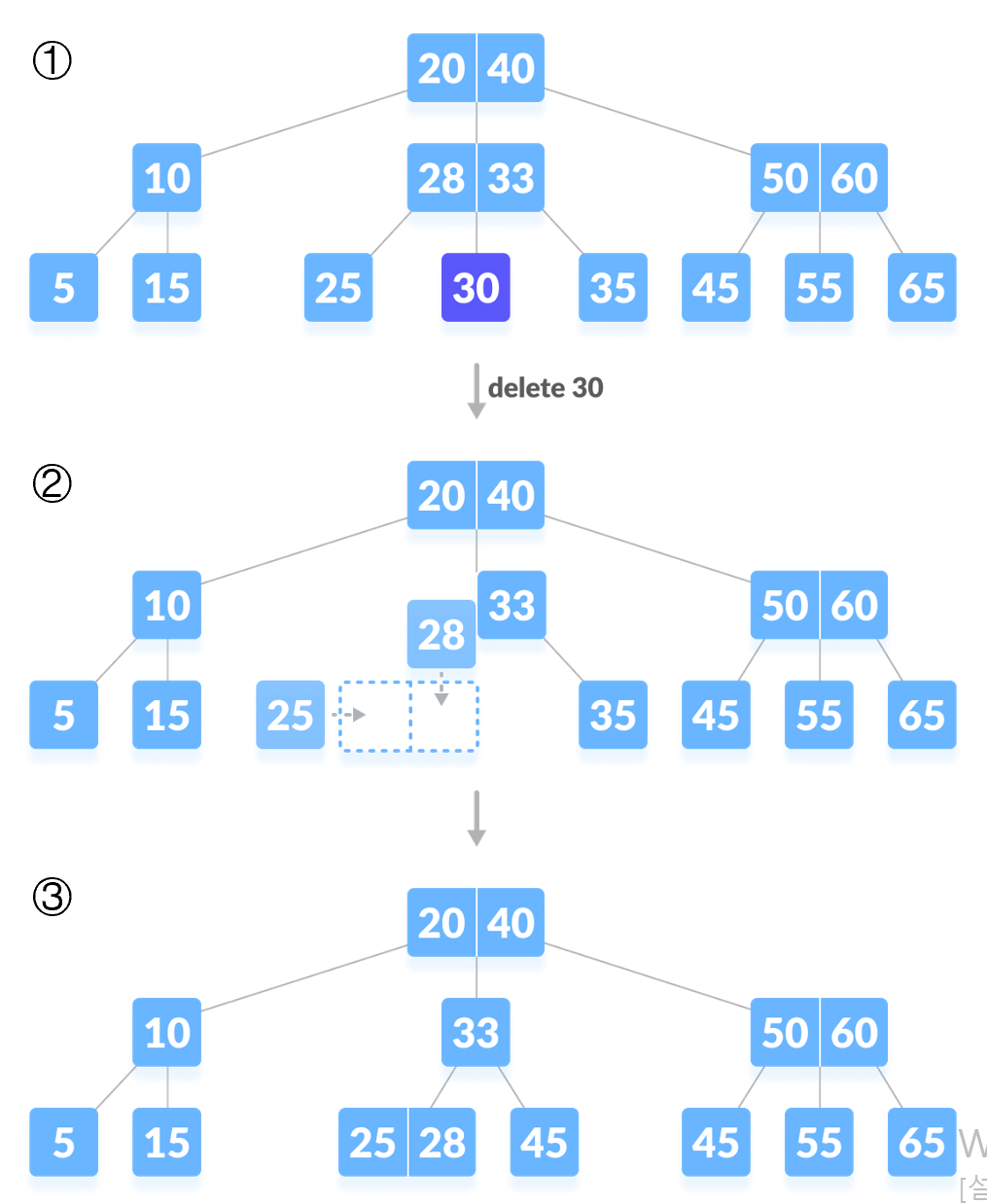
Case 2-1. 재조정이 필요하고 차용이 가능한 경우(M=2)
  • 아래 예시에서, ‘31’을 삭제하면 최소한의 키 수(M/2 - 1)보다 작아져서 재조정이 필요하다.
    • 키 수가 여유있는 형제 노드의 지원을 받는다.
      • 동생 노드(왼쪽 노드)를 보면 키가 ‘25, 28’로 여유가 있기 때문에 동생노드로부터 키를 지원 받는다. 바로 28로 옮기는 것이 아니라 B트리의 속성에 맞게 28은 부모노드로 옮기고 30을 내린다.

Case 2-2. 재조정이 필요하고 차용이 불가능한 경우(M=2)
  1. 동생이 있으면 동생 노드와 현재 노드 사이의 키를 부모로부터 내려 받는다
    • 그 키와 나의 키를 차례대로 동생에게 합친다.
    • 현재 노드를 삭제한다.
  2. 동생이 없으면 형 노드와 현재 노드 사이의 키를 부모로부터 내려받는다.
    • 부모로부터 받은 키와 형 노드의 키를 차례대로 나에게 합친다.
    • 형 노드를 삭제한다.
Case 2-3. 리프노드에서 삭제하고 재조정 해야하는 경우
  • 재조정 진행 이후 부모 노드에서 문제가 발생하여 다시 재조정을 해야하는 경우
  1. 부모가 루트 노드가 아니라면
    • 그 위치에서부터 다시 1번부터 재조정 진행
  2. 부모가 루트 노드이고 비어있다면
    • 부모 노드를 삭제한다.
    • 직전에 합쳐진 노드가 루트노드가 된다.

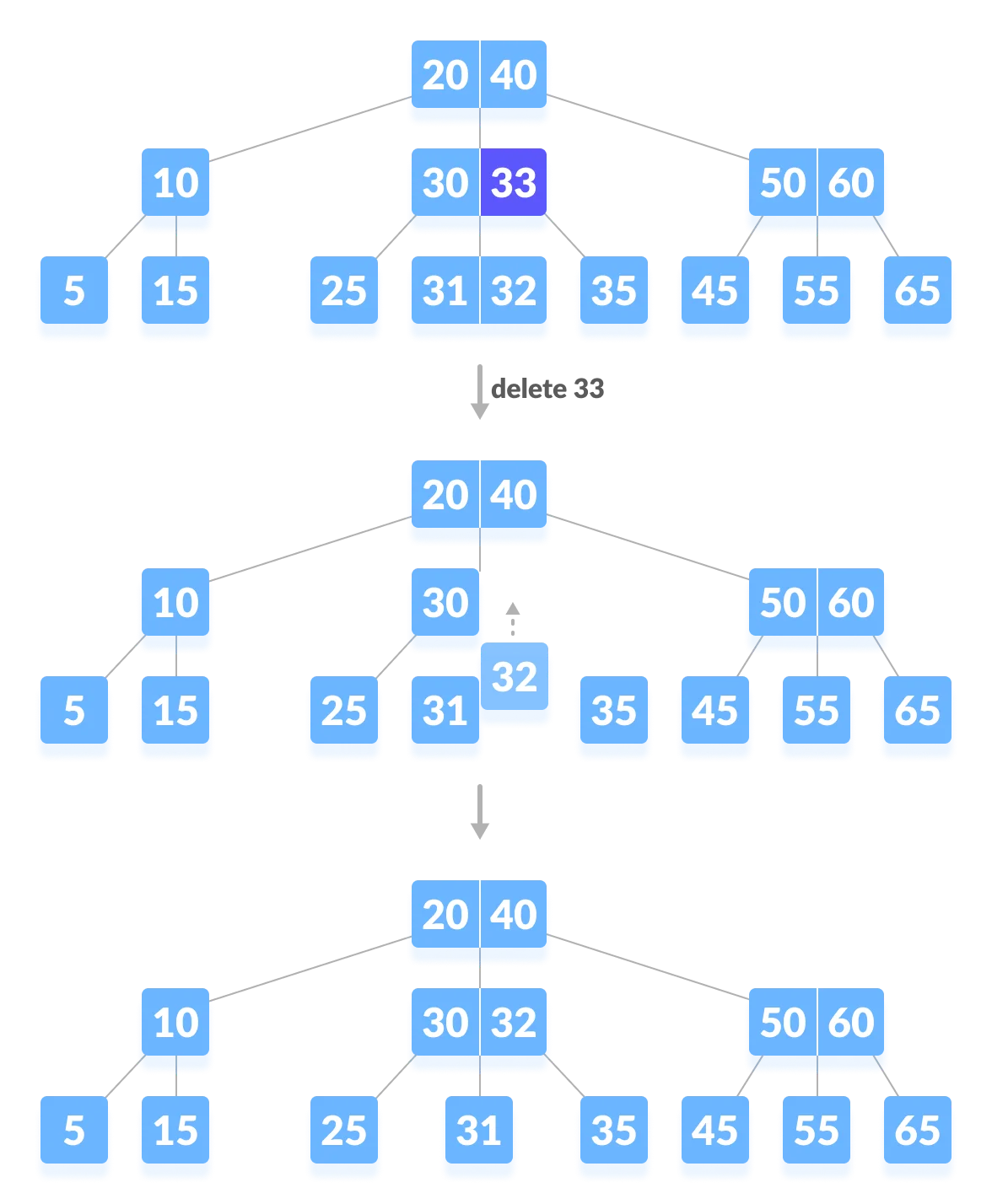
내부 노드에서 삭제(M=2)

  • 내부 노드에 있는 데이터를 삭제하려면 말단 노드에 있는 데이터와 위치를 바꾼 후 삭제한다.
  • 이후에는 Case2와 동일하게 진행

어떤 말단노드에 있는 데이터와 바꿀 것인가?
삭제할 데이터의 선임자나 후임자와 위치를 바꿔준다.

  • 선임자(predecessor): 나보다 작은 데이터들 중 가장 큰 데이터
  • 후임자(successor): 나보다 큰 데이터들 중 가장 작은 데이터

R트리, B트리를 다차원으로

R트리란?

R트리(R-Tree)는 다차원 공간에서 범위 검색 및 최근접 이웃 검색을 효율적으로 수행하기 위한 트리 자료구조이다. 여러 속성(다차원 데이터)을 인덱싱하고 각 속성에 대해 효율적인 탐색이 가능하도록 해주는 구조이다. 이 자료구조는 주로 지리 정보 시스템(GIS)이나 컴퓨터 그래픽스, 공간 데이터베이스 등에서 많이 사용된다.

R트리는 Antonin Guttman이 1984년에 제안한 자료구조로, B트리와 유사한 구조를 가지면서도 다차원 데이터를 처리할 수 있도록 각 노드가 특정 공간 영역을 나타내는 방식으로 동작한다.

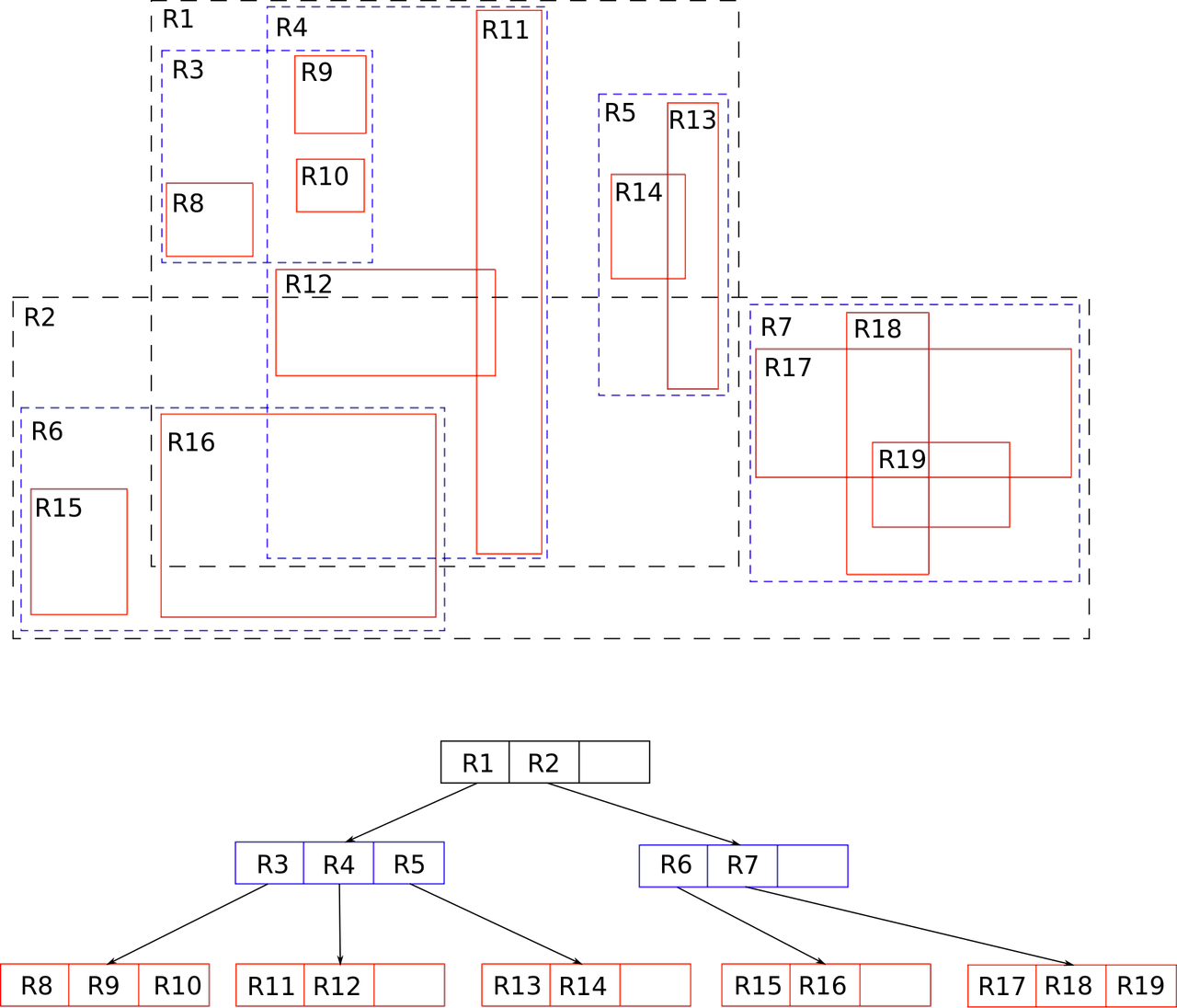
R트리 구조

R트리는 B트리와 비슷하게 균형 트리 구조를 가진다. 즉, 모든 리프 노드의 높이가 동일하며, 삽입과 삭제가 이루어질 때 트리가 재조정된다. 하지만 R트리는 각 노드가 특정 공간을 나타내는 사각형 영역 또는 초평면(Hyperplane)으로 구성된다. 이러한 사각형을 최소 경계 사각형(MBR: Minimum Bounding Rectangle)이라고 하며, 각 MBR이 겹치지 않도록 트리를 구성하여 다차원 데이터를 효율적으로 인덱싱한다.

  • 리프 노드: 실제 데이터를 포함하며, 각 데이터가 포함된 MBR을 가지고 있다.
  • 내부 노드: 하위 노드들을 포함하는 MBR을 가지고 있다. 즉, 하위 리프 노드 또는 다른 내부 노드들이 포함된 최소 경계 사각형이다.
  • 최상위 노드(Root): 전체 데이터를 포함하는 최소 경계 사각형을 가진다.

R트리 탐색 연산

R트리에서 탐색 연산은 특정 점 또는 영역이 트리 내에서 포함되어 있는지 여부를 확인하는 방식으로 이루어진다. 탐색 과정은 다음과 같다.

  1. 루트 노드에서 시작: 루트 노드의 MBR과 검색할 영역이 겹치는지 확인한다.
  2. 재귀적 탐색: 검색할 영역이 노드의 MBR과 겹칠 경우, 해당 노드의 자식 노드들에 대해 동일한 탐색을 반복한다.
  3. 리프 노드 도달: 리프 노드까지 도달하여 검색할 영역과 일치하는 데이터를 찾는다.

이러한 탐색은 일반적으로 범위 탐색, 포함 탐색, 교차 탐색, 근접 탐색 등 다양한 쿼리를 효율적으로 처리할 수 있다.

R트리 삽입 연산

R트리의 삽입 연산은 새로운 데이터를 적절한 위치에 삽입하고, 트리의 균형을 유지하는 방식으로 이루어진다. 다음은 삽입 연산의 기본 절차이다.

  1. 삽입할 리프 노드 탐색: 루트 노드에서 시작하여 새로운 데이터의 MBR이 가장 적합한(즉, 최소한의 영역 확장이 필요한) 리프 노드를 탐색한다.
  2. 데이터 삽입: 적절한 리프 노드를 찾은 후, 그 위치에 새로운 데이터를 삽입한다.
  3. 노드 분할(Overflow): 삽입된 리프 노드의 MBR 크기가 초과하면, 해당 리프 노드를 분할하여 부모 노드로 분할된 노드의 MBR을 올린다.
  4. 재조정: 부모 노드에서 MBR이 초과되면, 부모 노드 역시 분할을 반복한다. 최악의 경우 루트 노드까지 분할이 일어나 트리의 높이가 1 증가할 수 있다.

R트리 삭제 연산

R트리에서 삭제 연산은 다음과 같은 방식으로 수행된다.

  1. 삭제할 데이터 탐색: 루트 노드에서부터 삭제할 데이터를 포함하는 리프 노드를 탐색한다.
  2. 데이터 삭제: 삭제할 데이터를 찾으면, 리프 노드에서 해당 데이터를 삭제한다.
  3. 노드 재조정(Underflow): 삭제 후 리프 노드에 남아있는 데이터가 너무 적을 경우, 리프 노드를 삭제하고 형제 노드와 병합하거나 부모 노드의 MBR을 재조정한다.
  4. 트리 균형 유지: 노드 병합 또는 재조정이 발생할 경우, 부모 노드와의 MBR을 갱신하여 트리의 균형을 유지한다.

MBR 병합

R트리의 주요 특징 중 하나는 MBR 병합이다. 삽입, 삭제, 탐색 시에는 항상 노드의 MBR을 확인하고, 필요에 따라 병합 연산이 수행된다. 병합 연산의 기본 원칙은 다음과 같다.

  • 두 노드의 MBR이 중첩되면, 두 노드의 MBR을 하나로 병합하여 새로운 MBR을 생성한다.
  • 병합된 MBR이 다른 MBR들과의 관계를 유지할 수 있도록 트리를 재조정한다.

이 과정에서 MBR 병합의 효율성을 높이기 위해, R*-트리와 같은 다양한 변형 알고리즘이 개발되었다.

R트리 시간 복잡도

R트리의 시간 복잡도는 다음과 같다.

  • 탐색 연산: 평균적으로 $O(log N)$의 시간 복잡도를 가진다. 그러나 MBR이 겹치는 경우가 많으면 탐색 시간이 증가할 수 있다.
  • 삽입 연산: 평균적으로 $O(log N)$의 시간 복잡도를 가진다. 하지만 분할이 많이 일어날 경우 삽입 시간이 늘어날 수 있다.
  • 삭제 연산: 평균적으로 $O(log N)$의 시간 복잡도를 가진다. 삭제 후 병합 및 재조정이 많이 필요하면 시간이 증가할 수 있다.

R트리의 장점과 한계점

장점

  • 다차원 데이터의 범위 탐색 및 근접 탐색을 효율적으로 수행할 수 있다.
  • 삽입, 삭제, 탐색 연산이 모두 $O(log N)$ 시간 복잡도를 가지므로, 대용량 데이터 처리에 유리하다.
  • 지리 정보 시스템(GIS), 컴퓨터 그래픽스 등 공간 데이터의 처리에 적합하다.

한계점

  • MBR이 겹치는 경우가 많아지면, 탐색 성능이 급격히 저하될 수 있다.
  • 동적 데이터(잦은 삽입 및 삭제)의 경우, 빈번한 노드 분할 및 병합으로 인해 트리의 성능이 저하될 수 있다.
  • 트리의 분할 및 병합 연산이 복잡하여, 구현 및 유지보수가 어렵다.

마지막으로

R트리는 다차원 데이터를 처리할 때 매우 유용한 자료구조이다. 지리 정보 시스템, 컴퓨터 그래픽스, 공간 데이터베이스 등에서 다양한 쿼리를 효율적으로 처리할 수 있으며, B트리와 유사한 구조를 통해 데이터의 균형을 유지한다. 다만, MBR의 겹침과 동적 데이터 처리 시 성능 저하를 방지하기 위해 R*트리와 같은 변형 알고리즘도 함께 고려해볼 수 있다.

이상으로 BST와 다차원 인덱싱을 위한 다양한 트리 자료구조에 대해 알아보았다. 각 자료구조의 특징과 사용 사례를 이해하고, 자신의 프로젝트나 연구에 맞는 자료구조를 선택하는 것이 중요하다.

참고 문헌

댓글남기기

참고

멀티 쓰레딩 환경에서 캐시 미스에 대해

4 분 소요

멀티 쓰레딩 환경에서 캐시 미스에 대해 CPU 캐시의 구조 이번 포스팅에 앞서, numpy가 더 빠른 이유 - 캐시메모리 입장에서를 먼저 보고 오길 권장한다. CPU 캐시 메모리에 대한 대략적인 이해 후 이번 포스팅을 보는 것이 훨씬 이해에 도움이 될 것이다.

Randomized Quick Sort와 느낀 점

2 분 소요

Randomized Quick Sort와 느낀 점 Quick Sort Quick Sort는 분할정복 알고리즘(Divide & Conquer)으로서, pivot을 잡고 partiton 함수로 pivot보다 작은 item들은 왼쪽에, pivot보다 큰 item들은 오른쪽에...