Gaussian Mixture Model

Gaussian mixture model

Fundamental Concept

• It is used in clustering
• The data distribution is represented using the mean and variance of the data.
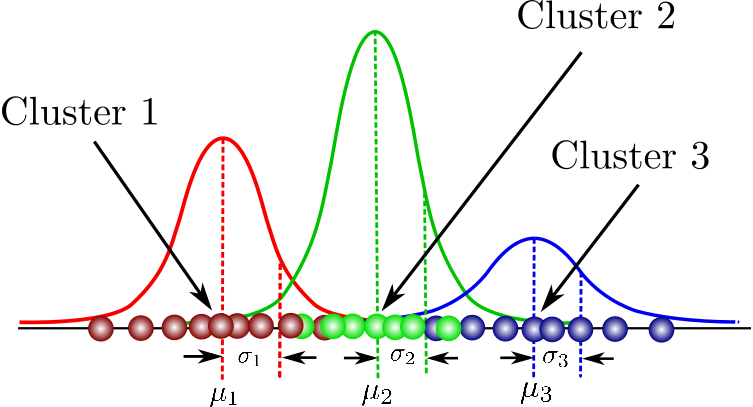
• The Gaussian distribution is mixed to represent complex data consisting of several groups.

Algorithm

• The Gaussian mixture model calculates the mean and variance for each Gaussian distribution at the data point.
  1. Initialize the mean and variance of each Gaussian distribution
  2. Calculate the weight of each data point from group to group
  3. Recompute parameters with weights obtained in course 2
  4. Repeat Steps 2 and 3 until each change in the average updated in Course 3 is sufficiently small

Sample Code

from sklearn.datasets import load_iris
from sklearn.mixture import GaussianMixture

data = load_iris()

model = GaussianMixture(n_components=3)
model.fit(data.data)

print(model.predict(data.data))
print(model.means_)
print(model.covariances_)

[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 0 2 0 2
 2 2 2 0 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0]
[[6.54639415 2.94946365 5.48364578 1.98726565]
 [5.006      3.428      1.462      0.246     ]
 [5.9170732  2.77804839 4.20540364 1.29848217]]
[[[0.38744093 0.09223276 0.30244302 0.06087397]
  [0.09223276 0.11040914 0.08385112 0.05574334]
  [0.30244302 0.08385112 0.32589574 0.07276776]
  [0.06087397 0.05574334 0.07276776 0.08484505]]

 [[0.121765   0.097232   0.016028   0.010124  ]
  [0.097232   0.140817   0.011464   0.009112  ]
  [0.016028   0.011464   0.029557   0.005948  ]
  [0.010124   0.009112   0.005948   0.010885  ]]

 [[0.2755171  0.09662295 0.18547072 0.05478901]
  [0.09662295 0.09255152 0.09103431 0.04299899]
  [0.18547072 0.09103431 0.20235849 0.06171383]
  [0.05478901 0.04299899 0.06171383 0.03233775]]]

참고문헌

• 秋庭伸也 et al. 머신러닝 도감 : 그림으로 공부하는 머신러닝 알고리즘 17 / 아키바 신야, 스기야마 아세이, 데라다 마나부 [공] 지음 ; 이중민 옮김, 2019.