Local Linear Embedding, LLE
A Dictionary Concept
- manifold : The low-dimensional manifold is a low-dimensional shape bent or twisted in a high-dimensional space.
Fundamental Concept
- LLE is an algorithm that represents a curved or twisted structure in a high-dimensional space as a simple structure in a low-dimensional space.
- LLE is one of the manifold learnings that dimensionally reduce data of nonlinear structures.
- LLE takes out the 2D structure hidden in the 3D space and represents it as 2D data.
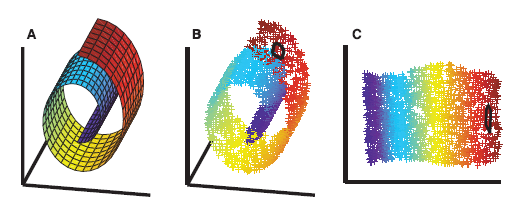
- Three steps in LLE
- Construct kNN graph
- Calculate the reconstruction of weights for reconstructing every point by its neighbors
- Use the obtained weights to embed the points in the low dimensional subspace
Algorithm
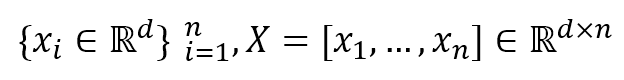
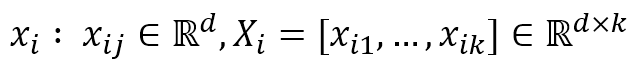
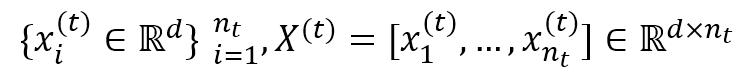
- training neighbors of x_i
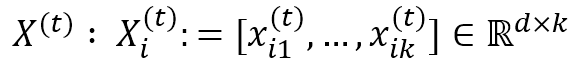
- LLE step1: Linear regional relationship modeling, Fix the sample and find the optimal weight.

- LLE step2: Reduce the dimension of preserving relationships, Fix the weights and find the optimal location of the sample image in the low-dimensional space.
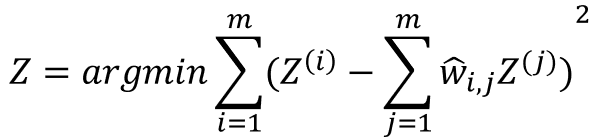
from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding
data, color = make_swiss_roll(n_samples = 1500)
model = LocallyLinearEmbedding(n_neighbors = 12,
n_components = 2)
model.fit(data)
print(model.transform(data))
[[ 0.02594418 -0.03808054]
[-0.00027408 0.05321859]
[ 0.025236 -0.00933512]
...
[ 0.00842605 0.04582885]
[ 0.02023957 0.00401955]
[ 0.03596786 -0.0481217 ]]
참고문헌
- 秋庭伸也 et al. 머신러닝 도감 : 그림으로 공부하는 머신러닝 알고리즘 17 / 아키바 신야, 스기야마 아세이, 데라다 마나부 [공] 지음 ; 이중민 옮김, 2019.

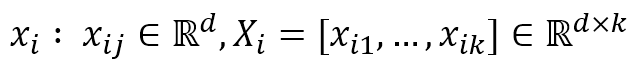
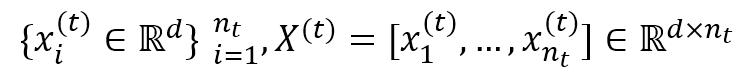
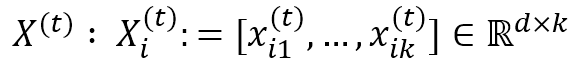

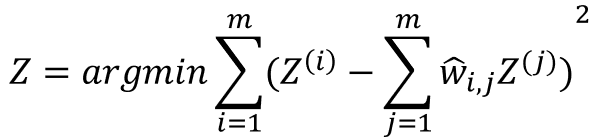


댓글남기기