Linear Regression
Linear Regression
Fundamental Concept
- A technique for modeling relationships in which dependent variables change large or small as independent variables grow.
- y = ax + b, a is called the inclination and b is called the y-intercept
Algorithm
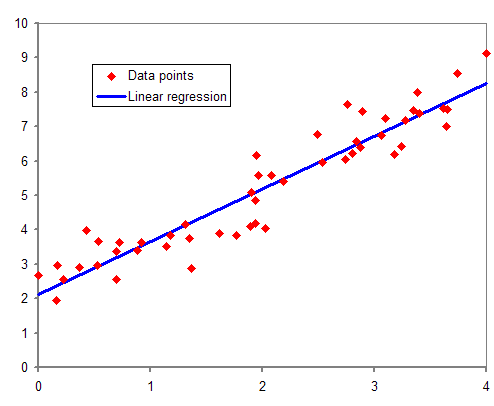
- Usually, in linear regression, the learning parameters a and b of the data points that are not on a straight line must be calculated.
-
Create a straight line to minimize the mean square error
- mean square error formula
- A function that defines the relationship between error and learning parameters is called a loss function.
- Linear regression finds a parameter with a minimum loss function value among various straight lines.
- Finding parameters that minimize loss function values is also a concept commonly used in guidance learning algorithms.
Sample Code
from sklearn.linear_model import LinearRegression
X = [[10.0], [8.0], [13.0], [9.0], [11.0], [14.0], [6.0], [4.0], [12.0], [7.0], [5.0]]
y = [8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68]
model = LinearRegression()
model.fit(X, y)
print(model.coef_)
print(model.intercept_)
y_pred = model.predict([[0], [1]])
print(y_pred)
[0.50009091]
3.0000909090909094
[3.00009091 3.50018182]
method of minimizing mean square error
| i | x | y |
|---|---|---|
| 0 | 2 | 1 |
| 1 | 3 | 5 |
| 2 | 6 | 3 |
| 3 | 7 | 7 |
| 선형회귀 | a | b | 평균제곱오차 |
|---|---|---|---|
| (a) | 0.823 | 0.706 | 2.89 |
| (b) | 4.5 | -0.125 | 5.83 |
Various Linear Regression and Nonlinear Regression
Linear Regression
| 선형회귀의 종류 | 함수 정의 예 |
|---|---|
| 단순선형회귀 | y=ax+b |
| 다중선형회귀 | ax+by+cz=d |
| 다항회귀 | y=ax^2+bx+c |
- Since polynomial regression is not linear, it may be awkward to call it linear regression, but because it is linear regression for learning parameters rather than independent variables, polynomial regression is also included in linear regression.
Nonlinear Regression
- y = e^x
- y = 1/x
참고문헌
- 秋庭伸也 et al. 머신러닝 도감 : 그림으로 공부하는 머신러닝 알고리즘 17 / 아키바 신야, 스기야마 아세이, 데라다 마나부 [공] 지음 ; 이중민 옮김, 2019.

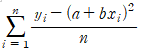
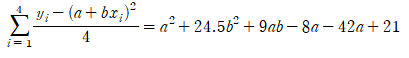

댓글남기기