SVM

SVM (Support Vector Machine)

Fundamental Concept

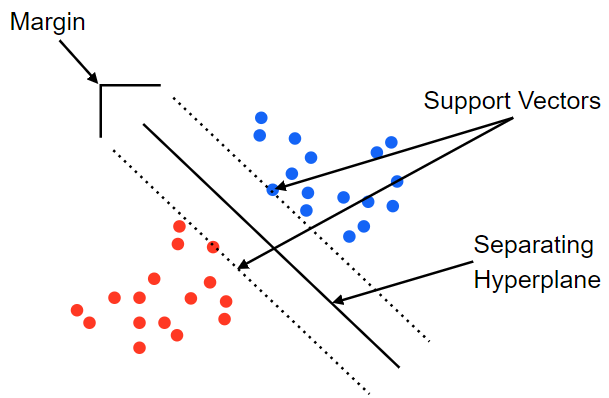
• The decision boundaries obtained by SVM maximize margin between groups, so learn to have no points belonging to the boundaries and classify them more clearly than logistic regression.

Algorithm

• SVM deals with the problem of binary classification of planes assuming linear and complete classification is possible.
• Maximize the margin between groups to obtain a good decision boundary to classify.

Sample Code

from sklearn.svm import LinearSVC
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

centers = [(-1, -0.125), (0.5, 0.5)]

X, y = make_blobs(n_samples = 50, n_features = 2, centers = centers, cluster_std = 0.3)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)

model = LinearSVC()

model.fit(X_train, y_train)
y_pred = model.predict(X_test)
accuracy_score(y_pred, y_test)

1.0

Margin and Support vector

• If the margin does not contain data, it is called hard margin.
• Allowing some data to be contained in margin is called soft margin.
• Learning data is divided into three categories.
  • data outside margin: data outside the margin based on the decision boundary
  • margin data: data for determining margin based on decision boundaries
  • data inside margin: data that are in margin or misclassified based on the boundary of the boundaries

Hard margin and Soft margin

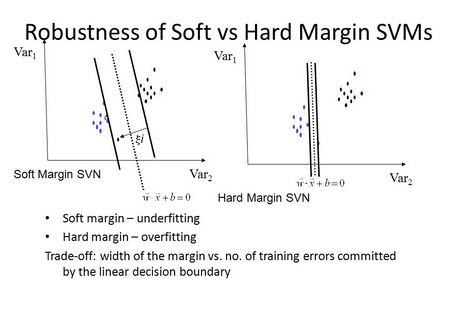
• The left graph using soft margin is not affected by the fact that the learning results are far away.
• The graph on the right using hard margin is greatly influenced by the point far away.
• How much data in the margin is allowed in soft margin follows the hyperparameters set by the person himself.

참고문헌

• 秋庭伸也 et al. 머신러닝 도감 : 그림으로 공부하는 머신러닝 알고리즘 17 / 아키바 신야, 스기야마 아세이, 데라다 마나부 [공] 지음 ; 이중민 옮김, 2019.