SVM using kernel

SVM (Support Vector Macnine) Using Kernel technique

Fundamental Concept

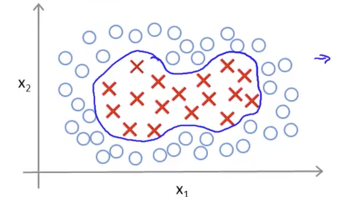
• In SVM, it is difficult to classify data in which the boundary of each label is curved because the decision boundary is a straight line.
• Complex decision boundaries can be learned by applying kernel techniques to SVM.

Algorithm

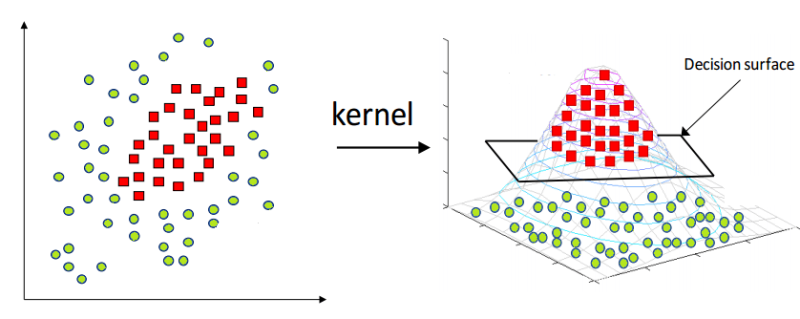
• kernel technique: linear regression after transferring data to another feature space
• conditions required to allow linear separation of data that cannot be linearly separated
  • There is a higher dimension space than the learning data, and each point of the learning data corresponds to a point of the higher dimension space.
  • Points corresponding to learning data in a high-dimensional space can be linearly separated, and actual learning data is projection in a high-dimensional space.

Sample Code

from sklearn.svm import SVC
from sklearn.datasets import make_gaussian_quantiles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

X, y = make_gaussian_quantiles(n_features = 2, n_classes = 2, n_samples = 300)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)

model = SVC(gamma = 'auto')

model.fit(X_train, y_train)
y_pred = model.predict(X_test)
accuracy_score(y_pred, y_test)

0.9666666666666667

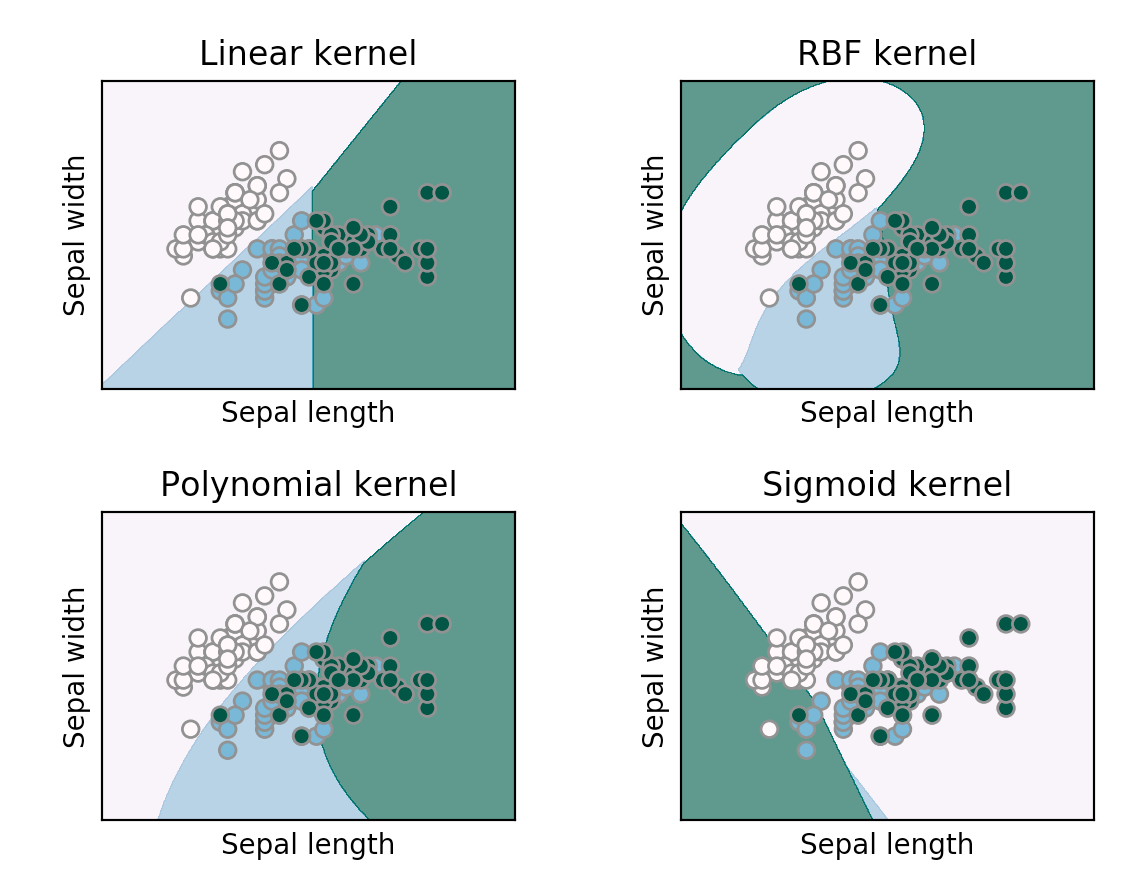
difference in learning outcomes using kernel functions

참고문헌

• 秋庭伸也 et al. 머신러닝 도감 : 그림으로 공부하는 머신러닝 알고리즘 17 / 아키바 신야, 스기야마 아세이, 데라다 마나부 [공] 지음 ; 이중민 옮김, 2019.