Juyeong Shin

KHU CSE 19
KHU DKE Lab.

8 분 소요

Semi-Supervised Classification With Graph Convolutional Networks, ICLR 2017

Graph Convolutional Networks (GCN)을 이용한 준지도학습 분류

저자

  • Thomas N.Kipf
  • Max Welling

0. 사전 지식

1. 테이블 데이터

  • Table 형태, 우리가 흔히 생각하는 Excel Chart이다.
  • 다른 말로, Tabular Data라 한다.

Tabular_Data

2. 그래프 데이터

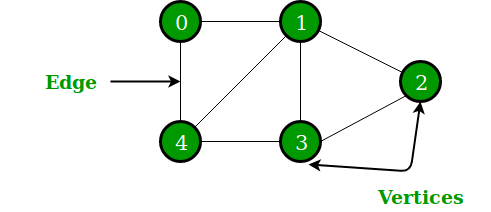
  • Graph 형태, 위 예시 테이블에서 각 행(row)이 노드(vertex)가 되고, 연관이 있는 경우 엣지(edge)를 만든다.

Graph_Data

3. 그래프 데이터 저장 방식

  • 인접행렬 (Adjacency Matrix)
    • 그래프의 노드 갯수가 N개 라고 하자
    • 그러면 인접행렬의 크기는 $N \times N$이 된다.
    • 각 행고 열은 해당 노드의 index가 된다.
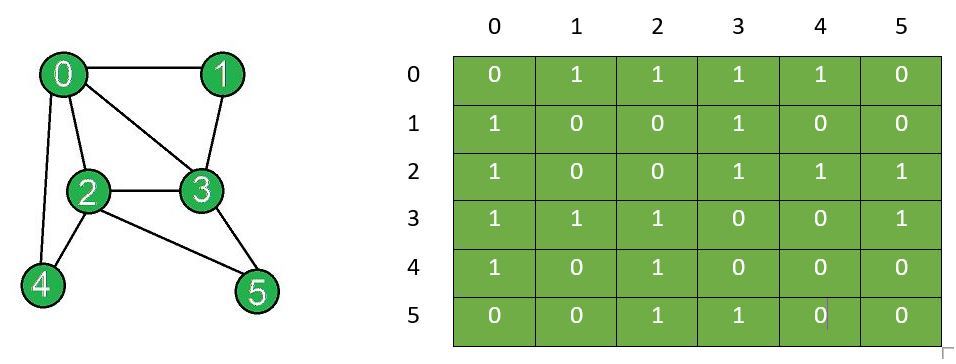
    • 아래 그림과 같이, 0번 노드가 1, 2, 3, 4와 연결되어 있으면, 연결이 되어있다는 의미에서 1로 표기되고, 0번 노드가 자기 자신과 5번 노드와는 연결되어 있지 않으므로, 0으로 표기된다.

Adjacency_Matrix

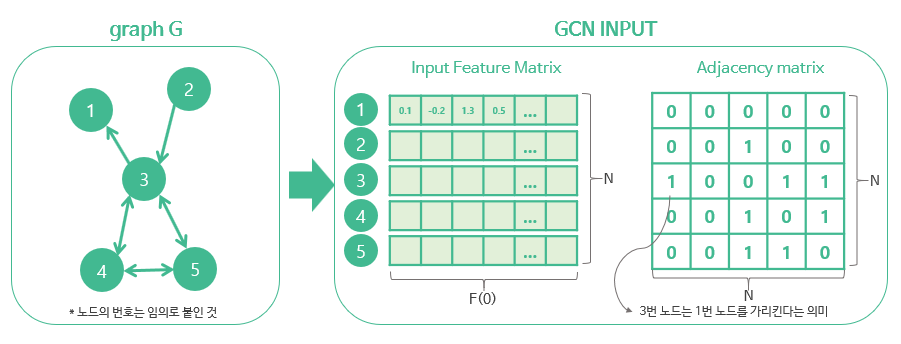
  • Graph Feature Matrix
    • 그래프 노드들의 피쳐(feature, attribute)들을 노드 index 순서대로 나열한 것
    • 아래 그림 참조

Feature_Matrix

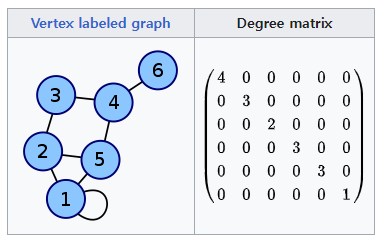
  • Graph Degree Matrix
    • 각 노드가 얼마나 많은 엣지를 가지고 있는지, 즉, 얼마나 많은 이웃 노드를 가지고 있는지 계산한 행렬
    • 인접행렬 행들의 모든 요소를 더한 값이 해당 노드의 Degree가 됨
    • 기본적으로, Degree Matrix는 대각 성분에 해당 노드의 Degree를 나타냄

Degree_Matrix

1. Introduction

1. 풀고자 하는 Task

  • Node Classification: 노드 분류
  • Semi-Supervised: 노드의 일부만 labeling 되어 있음

2. Notation

  • 그래프 (Graph): $G=(V, E)$
    • $V$: 그래프의 노드 혹은 정점 (Vertex), $v_i \in V$
    • $E$: 그래프의 엣지 혹은 간선 (Edge), $(v_i, v_j) \in \epsilon$
  • 인접행렬 (Adjacency Matrix): $A \in \mathcal{R}^{N \times N}$
  • 피쳐행렬 (Feature Matrix): $X$
  • 차수행렬 (Degree Matrix): $D_{ii} = \sum_{j} A_{ij}$
  • Neural Network Model Function: $f(\cdot)$, $f(X, A)$
  • 손실 함수 (Loss Function): $L = L_0 + L_{reg}$
    • $L_0$: 지도학습 손실 함수, i.e. Cross-Entropy Loss
    • $L_{reg}$: graph Laplacian Regularization, 지금은 엣지 간의 가중치를 조정하기 위한 항(term)이라는 정도로만 이해
  • Unnormalized graph Laploacian Regularization: $\Delta=D-A$
    • 학습을 통해 조정된 엣지 가중치의 변화량을 측정하기 위한 항(term)

3. Contribution

  • spectral graph convolution 연산에 근사하는 layer-wise propagation rule 제안
  • 즉, spectral convolution 연산을 근사시킬 수 있는 세로운 수식을 제안함으로써, 연산 시간을 줄임
  • 기존 GNN 모델에 비해 fast하고 scalable한 모델 제안

2. 핵심 아이디어

Aggregate

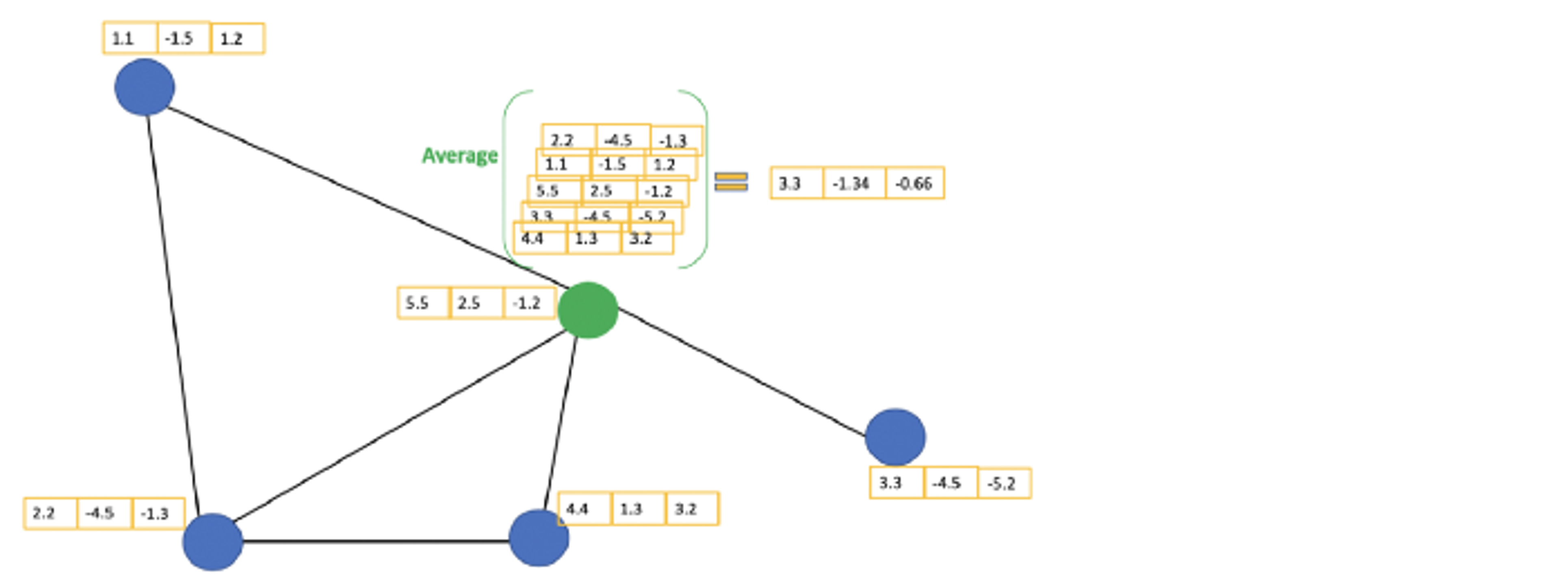
gcn_main_idea

  • 위 그림의 초록색 노드를 고려
    1. 주변 이웃 노드의 feature value를 모음
    2. 그 feature value들의 평균을 구함
    3. 구해진 평균을 이용해 MLP(Multi-Layer Perceptron) 학습

GCN Layer

2_layer_gcn

2. Fast Approximate Convolutions on Graphs

1. Layer-Wise Linear Model

  • graph-based neural network model: $f(X, A)$
  • multi-layer Graph Convolutional Network
  • 최종 수식은 아래와 같음
\[H^{(l+1)}=\sigma({\tilde{D}}^{-1/2} \tilde{A} {\tilde{D}}^{-1/2} H^{(l)} W^{(l)})\]
  • $\tilde{A} = A + I_N$
    • 즉, $\tilde{A}$는 기존 그래프에다가 자기 자신에 대한 엣지를 추가한 것
    • 인접행렬의 모든 대각 성분에 $I_N$을 더하면 자기 자신을 가리키는 엣지가 되기 때문
    • 이때, $I_N$은 $N \times N$ 크기의 단위행렬
  • $D_{ii} = \sum_{j} A_{ij}$
    • 차수행렬, diagonal degree matrix
    • 대각성분을 제외한 모든 성분은 0
    • 각 노드에 해당하는 대각 성분에 해당 노드의 차수가 들어감
  • $\sigma(\cdot)$: 활성화 함수
    • 예를 들면, $RELU(\cdot) = max(0, \cdot)$ 와 같은 활성화 함수가 있음
  • $H^{(l)} \in {\mathcal{R}}^{N \times D}$
    • $l$ 번째 레이어의 활성화 함수까지 통과한 결과
    • $H^{(0)} = X$
    • $H^{(1)} = \sigma({\tilde{D}}^{-1/2} \tilde{A} {\tilde{D}}^{-1/2} H^{(0)} W^{(0)})$

2. Wrong Picture about GCN

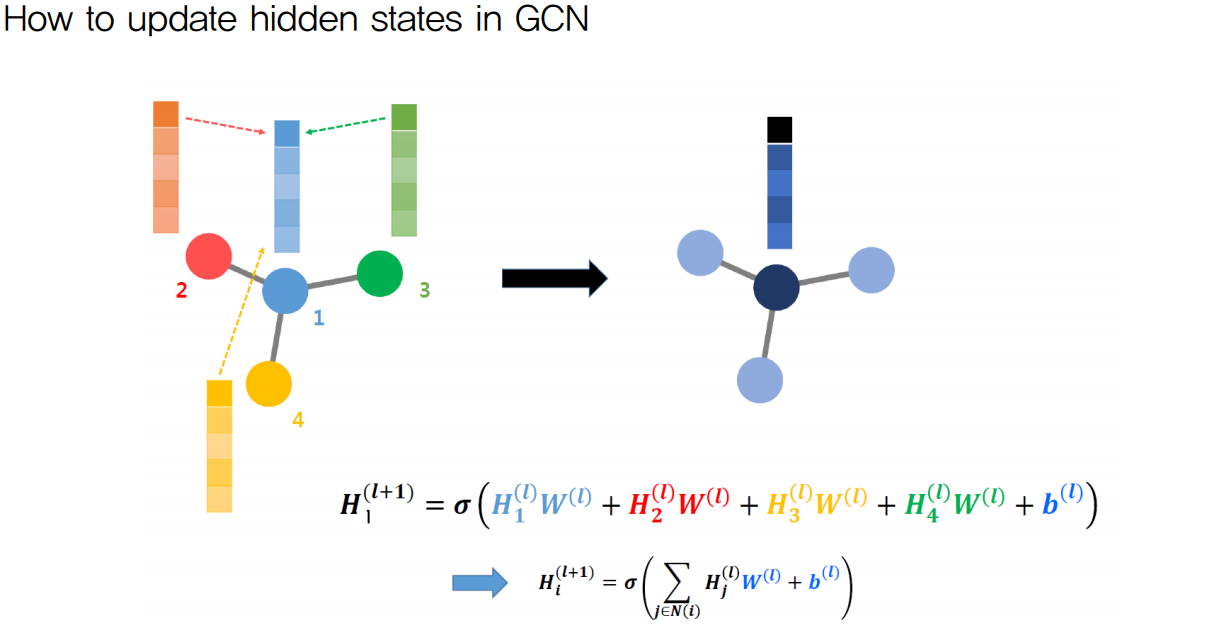
update_hidden_state

  • 위 그림의 수식에서 W는 Neural Network (Convolution을 배제한) Weight를 의미
  • l은 l번째 Layer를 의미
  • H는 Hidden State (각 레이어를 거친 뒤의 node feature matrix)

  • 그러나, GCN은 위 그림과는 차이가 존재

  • 우선, $H_1^{(l)}$ 은 1번 노드의 Feature Matrix (혹은 Hidden State Matrix)
  • 마찬가지로, $H_2^{(l)}$ 은 2번 노드의 Feature Matrix (혹은 Hidden State Matrix)
  • 이때, 각 노드 별로 차수(degree)가 다르므로 각 hidden state가 더해지는 가중치가 다름
    • 이때 말하는 가중치는, Adjacency Matrix를 정규화한 엣지 가중치, Neural Network 가중치가 아님
    • 따라서, 위 수식에 각 노드별로 어느 만큼의 가중치를 주어 Node Feature를 업데이트 할 것인지 기입해야함
    • 즉, 가중치 항을 추가해야함
  • 또한, 모든 Feature Vector가 같은 Weight Matrix를 공유하는 것은 사실 (Weight Sharing)
    • 그러나, 위 수식처럼 같은 Weight Vector를 공유하는 것은 아님
    • GCN에서 Weight Matrix는 가중치 열벡터의 나열로 구성되는데, 각 열벡터는 서로 다른 값을 가짐

3. Correct Explanation about GCN

  1. $\hat{A} = I_N + {D}^{-1/2} A {D}^{-1/2}$
    • 우선 $\hat{A} = I_N + {D}^{-1/2} A {D}^{-1/2}$ 를 통해 정규화된 Adjacency Matrix를 계산
    • 위 수식은, 각 엣지 별로 다른 가중치를 주어서 어느 노드의 Feature Vector를 어느 만큼의 가중치를 주어 Convolution 연산을 할 것인지 결정
    • $I_N$은 본인 스스로의 Node Feature도 연산하여야하기 때문에 추가
  2. $\hat{A} \times H^{(l)}$
    • 정규화된 Adjacency Matrix($\hat{A}$)과 Hidden State Vector($H^{(l)}$) 을 곱하여 각 엣지 가중치 만큼 덧셈 연산 수행
    • 위 덧셈 연산 수행이 Convolution 연산
  3. $W^{(l)}$
    • Convolution 된 각 Node Feature Vector와 Neural Network Weight Matrix를 곱하는 연산
    • Node Feature Vector의 원소 하나가 우리가 흔히 생각하는 Neural Network 그림의 perceptron 1개가 됨
    • Node Feature Vector가 50차원이면 Neural Network Perceptron은 50개
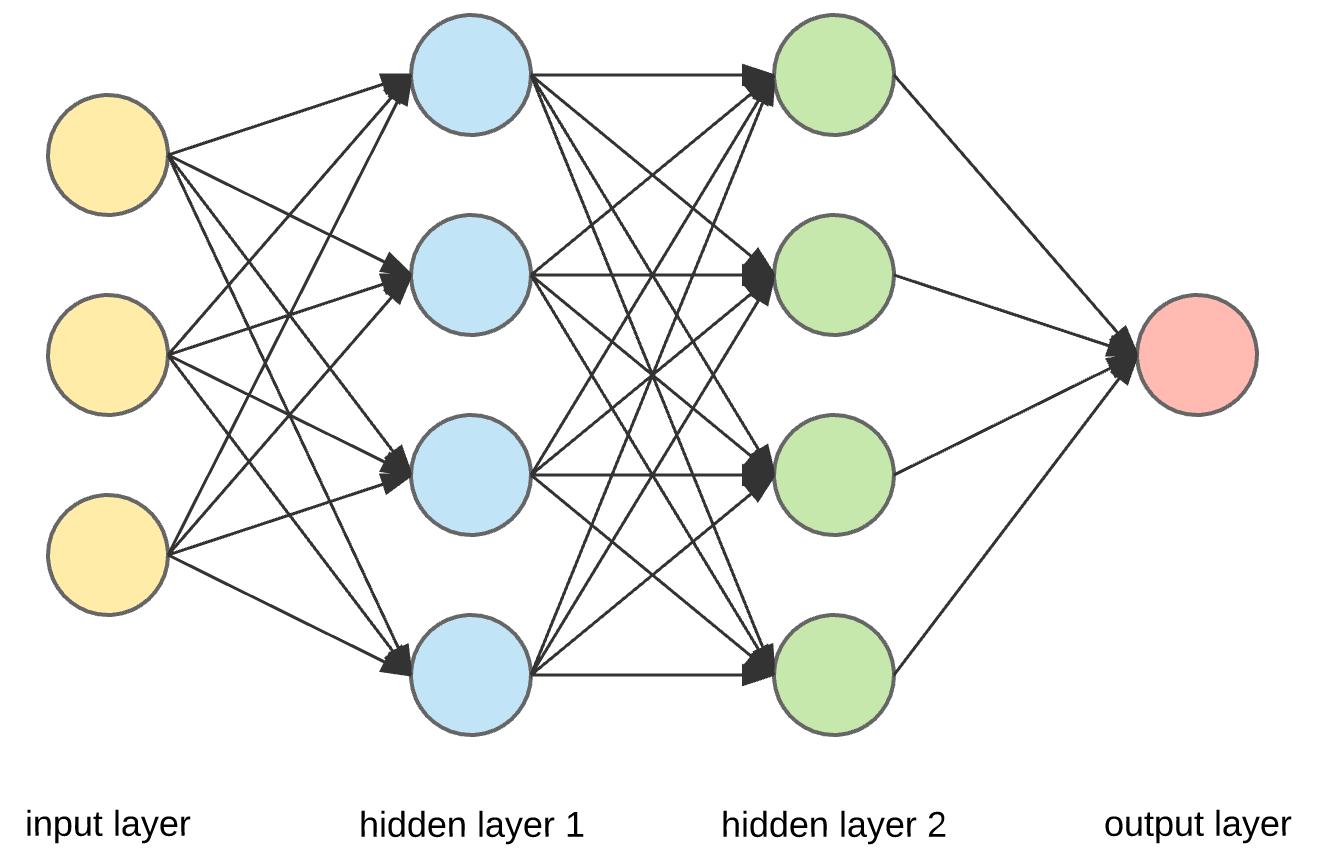
    • Weight Matrix $W$는 아래 Neural Network 그림에서 두 레이어 사이의 화살표들에 대응함
    • 아래 그림에서, input layer는 3차원 벡터, hidden layer는 4차원 벡터
    • 따라서, 아래 그림에서, Weight Matrix 사이즈는 $3 \times 4$

nn

4. About $\hat{A} = I_N + D^{-1/2} A D^{-1/2}$

  • GCN은 기본적으로 무향 그래프를 사용 (undirected graph)
  • 또한, Graph Weight는 고려하지 않음
  • Convolution 연산 시, 각 노드의 계수 (각 노드가 얼마나 많은 이웃을 가지고 있는가)를 무시하고 무작정 더하면, 많은 이웃을 가진 노드는 그저 큰 값의 feature vector를, 적은 이웃을 가진 노드는 그저 작은 값으 feature vector를 가지게 될 것임
  • 따라서, 위로 인해 발생할 수 있는 오류를 해결하기 위해 $\hat{A} = I_N + D^{-1/2} A D^{-1/2}$ 연산을 수행
  • 위 방법은 전체 그래프를 한번에 학습해야 한다는 단점을 가짐
  • 이에 본 논문은 Fast Approximate Convolution 수식을 제안하였으며, 그 수식이 $\hat{A} = I_N + D^{-1/2} A D^{-1/2}$
  • 위 수식이 본 논문이 제안하는 가장 핵심적인 수식 (기존 Spectral GCN과의 주된 차이점)
  • 그러나, 여전히 mini-batch 학습은 불가능

5. Two-Layer Forward Model Example

\[Z=f(X, A)=softmax(\hat{A}ReLU(\hat{A}XW^{(0)})W^{(1)})\] \[H^{(0)}=ReLU(\hat{A}XW^{(0)})\] \[Z=softmax(\hat{A}H^{(0)}W^{(1)})\]

3. Calculating Example

1. Define Graph and Node Feature

  • example graph

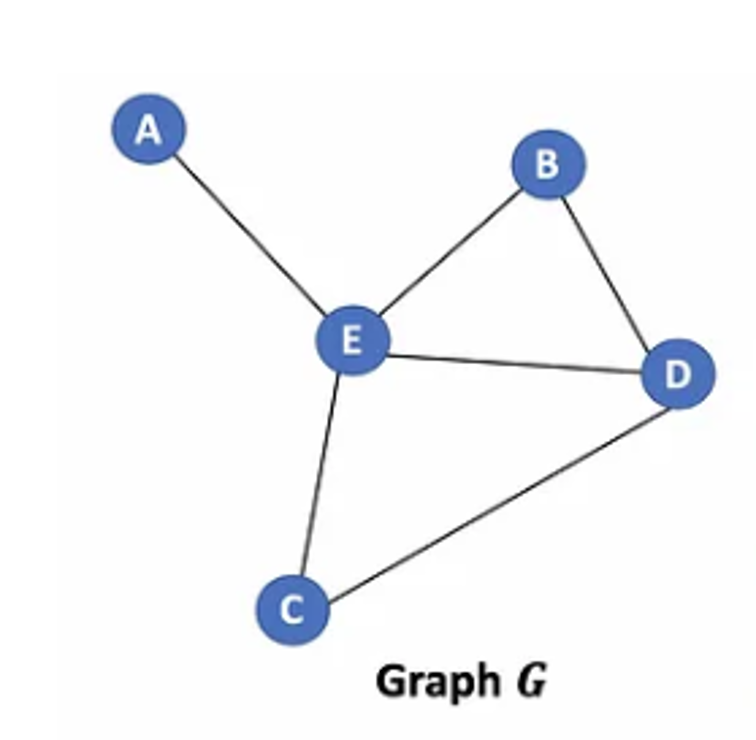
graph

  • example adjacency matrix
  A B C D E
A 0 0 0 0 1
B 0 0 0 1 1
C 0 0 0 1 1
D 0 1 1 0 1
E 1 1 1 1 0
  • example node feature matrix
  feat1 feat2 feat3
A -1.1 3.2 4.2
B 0.4 5.1 -1.2
C 1.2 1.3 2.1
D 1.4 -1.2 2.5
E 1.4 2.5 4.5

2. First-Layer Calculating Example (Without Activation Function)

  • adjacency matrix, $A$

\[A = \begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \end{bmatrix}\]

  • $\tilde{A}$

\[\tilde{A} = I_N + A\] \[\tilde{A} = \begin{bmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \end{bmatrix}\]

  • diagonal degree matrix, $D$

\[D = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 4 \end{bmatrix}\]

  • $\tilde{D}$

\[\tilde{D} = \sum_j{\tilde{A}_{ij}}\] \[\tilde{D} = \begin{bmatrix} 2 & 0 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 & 0 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 \\ 0 & 0 & 0 & 0 & 5 \end{bmatrix}\]

  • ${\tilde{D}}^{-1/2}$

\[{\tilde{D}}^{-1/2} = \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & 0 & 0 & 0 \\ 0 & 0 & \frac{1}{\sqrt{3}} & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{2} & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{\sqrt{5}} \end{bmatrix}\]

  • $\hat{A} = {\tilde{D}}^{-1/2} \tilde{A} {\tilde{D}}^{-1/2}$

\[{\tilde{D}}^{-1/2} \tilde{A} = \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & 0 & 0 & 0 \\ 0 & 0 & \frac{1}{\sqrt{3}} & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{2} & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{\sqrt{5}} \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 & 0 & \frac{1}{\sqrt{2}} \\ 0 & \frac{1}{\sqrt{3}} & 0 & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \\ 0 & 0 & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \\ 0 & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} \end{bmatrix}\] \[\hat{A} = {\tilde{D}}^{-1/2} \tilde{A} {\tilde{D}}^{-1/2} = \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 & 0 & \frac{1}{\sqrt{2}} \\ 0 & \frac{1}{\sqrt{3}} & 0 & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \\ 0 & 0 & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \\ 0 & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} \end{bmatrix} \cdot \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & 0 & 0 & 0 \\ 0 & 0 & \frac{1}{\sqrt{3}} & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{2} & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{\sqrt{5}} \end{bmatrix}\] \[= \begin{bmatrix} \frac{1}{2} & 0 & 0 & 0 & \frac{1}{\sqrt{6}} \\ 0 & \frac{1}{3} & 0 & \frac{1}{2\sqrt{3}} & \frac{1}{3} \\ 0 & 0 & \frac{1}{3} & \frac{1}{2\sqrt{3}} & \frac{1}{3} \\ 0 & \frac{1}{2\sqrt{3}} & \frac{1}{2\sqrt{3}} & \frac{1}{4} & \frac{1}{2\sqrt{3}} \\ \frac{1}{\sqrt{6}} & \frac{1}{3} & \frac{1}{3} & \frac{1}{2\sqrt{3}} & \frac{1}{3} \end{bmatrix}\]

  • $\hat{A} X$

    \(\hat{A} X = \begin{bmatrix} \frac{1}{2} & 0 & 0 & 0 & \frac{1}{\sqrt{6}} \\ 0 & \frac{1}{3} & 0 & \frac{1}{2\sqrt{3}} & \frac{1}{3} \\ 0 & 0 & \frac{1}{3} & \frac{1}{2\sqrt{3}} & \frac{1}{3} \\ 0 & \frac{1}{2\sqrt{3}} & \frac{1}{2\sqrt{3}} & \frac{1}{4} & \frac{1}{2\sqrt{3}} \\ \frac{1}{\sqrt{6}} & \frac{1}{3} & \frac{1}{3} & \frac{1}{2\sqrt{3}} & \frac{1}{3} \end{bmatrix} \cdot \begin{bmatrix} -1.1 & 3.2 & 4.2 \\ 0.4 & 5.1 & -1.2 \\ 1.2 & 1.3 & 2.1 \\ 1.4 & -1.2 & 2.5 \\ 1.4 & 2.5 & 4.5 \end{bmatrix}\)

\[= Aggregated Feature Matrix\]

  • $H^{(1)} = \hat{A} X W$

\[H^{(1)} = \hat{A} X W\]

4. Results

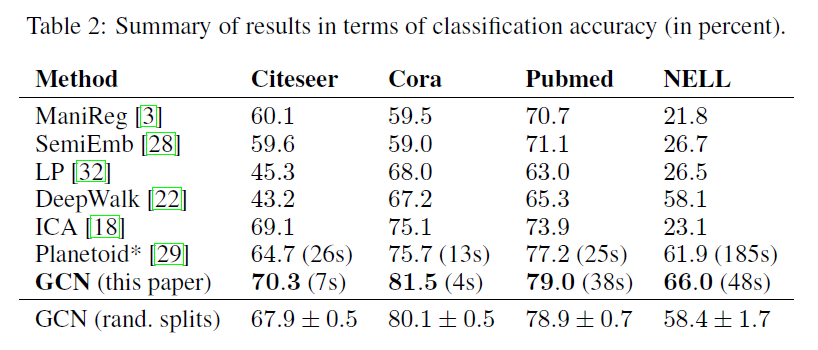
results

5. Conclusion

  • 기존 Graph Machine Learning 기법들에 비하여 효율적이면서도 성능이 좋은 모델을 제안

6. Limitation

  • Minibatch-Training이 여전히 쉽지 않음
    • 메모리 부족 문제 발생
  • 유향 그래프 학습에 대한 고려 없음
  • edge feature 학습 고려 없음
  • 제한적 상황에 맞춘 Convolution 근사식을 제공
    • 범용적인 그래프(유향, weighted …)에 대한 제안 없음

7. 참고문헌

댓글남기기

참고

멀티 쓰레딩 환경에서 캐시 미스에 대해

4 분 소요

멀티 쓰레딩 환경에서 캐시 미스에 대해 CPU 캐시의 구조 이번 포스팅에 앞서, numpy가 더 빠른 이유 - 캐시메모리 입장에서를 먼저 보고 오길 권장한다. CPU 캐시 메모리에 대한 대략적인 이해 후 이번 포스팅을 보는 것이 훨씬 이해에 도움이 될 것이다.

Randomized Quick Sort와 느낀 점

2 분 소요

Randomized Quick Sort와 느낀 점 Quick Sort Quick Sort는 분할정복 알고리즘(Divide & Conquer)으로서, pivot을 잡고 partiton 함수로 pivot보다 작은 item들은 왼쪽에, pivot보다 큰 item들은 오른쪽에...

BST(Binary Search Tree)와 KD트리 그리고 B트리와 R트리

12 분 소요

BST(Binary Search Tree)와 KD트리 그리고 B트리와 R트리 트리를 이용한 인덱싱 기법들.. 근데 이제, 다차원을 곁들인 자료구조를 공부한 적이 있다면 BST(Binary Search Tree, 이진탐색트리)도 배웠을 것이다.