Tree-KG: An Expandable Knowledge Graph Construction Framework for Knowledge-intensive Domains
Tree-KG: An Expandable Knowledge Graph Construction Framework for Knowledge-intensive Domains
논문 정보
- Songjie Niu, Kaisen Yang, Rui Zhao, Yichao Liu, Zonglin Li, Hongning Wang, Wenguang Chen
- ACL 2025: The 63rd Annual Meeting of the Association for Computational Linguistics
- Tsinghua University, Tsinghua Shenzhen International Graudate School
1. Introduction
- 과학 연구처럼 복잡하고 전문적인 분야의 지식을 체계적으로 정리하기 위해, Tree-KG라는 새로운 지식 그래프(Knowledge Graph, KG) 자동 구축 프레임워크를 제안
- 인간이 교과서 목차처럼 지식을 계층적으로 구성하는 방식에서 영감을 얻어 이를 자동화 하는 것
핵심 문제
- 과학, 의료, 법률 등 지식 집약적 분야에서는 방대한 데이터를 구조화하여 의사결정에 활용하는 것이 중요
- 지식 그래프(KG)가 좋은 해결책지만, 이 분야들은 내용이 너무 복잡하고 빠르게 변해서 KG를 만드는 데 많은 수작업과 노력이 필요
기존 연구의 한계점
- 규칙 기반 시스템 (Rule-based systems)
- 높은 정확도를 보여주나, 확장성과 일반화 능력이 부족, 새로운 상황에 취약
- 반대로, DL 및 임베딩 기반은 확장성을 위한 별도의 모델 설계 혹은 유사도 연산을 통한 일반화 능력이 우수
- 지도 학습 모델 (Supervised learning methods)
- 고품질의 데이터셋을 만드는 데 많은 비용과 노력이 필요
- 학습 데이터에 대한 의존도가 높아 적응성이 떨어짐
- LLM 기반 방법
- 자동화에 유용
- 잘 정의된 지식 구조나 의미적 일관성이 부족 (hallucination이 그대로 반영된 KG를 구축)
- 지식을 점진적으로 확장하는 자체 매커니즘이 없어 확장성에 한계가 존재
핵심 아이디어
- 인간이 교과서 목차처럼 지식을 계층적으로 구성하는 방식에서 영감을 얻음
- 실제 물리 교과서 데이터를 분석한 결과, 교과서상 가까운 위치에 있는 개념일수록 관계성이 강하다는 사실을 확인
-
이를 바탕으로 교과서의 구조를 적극적으로 활용하는 ‘Tree-KG’ 프레임워크를 개발
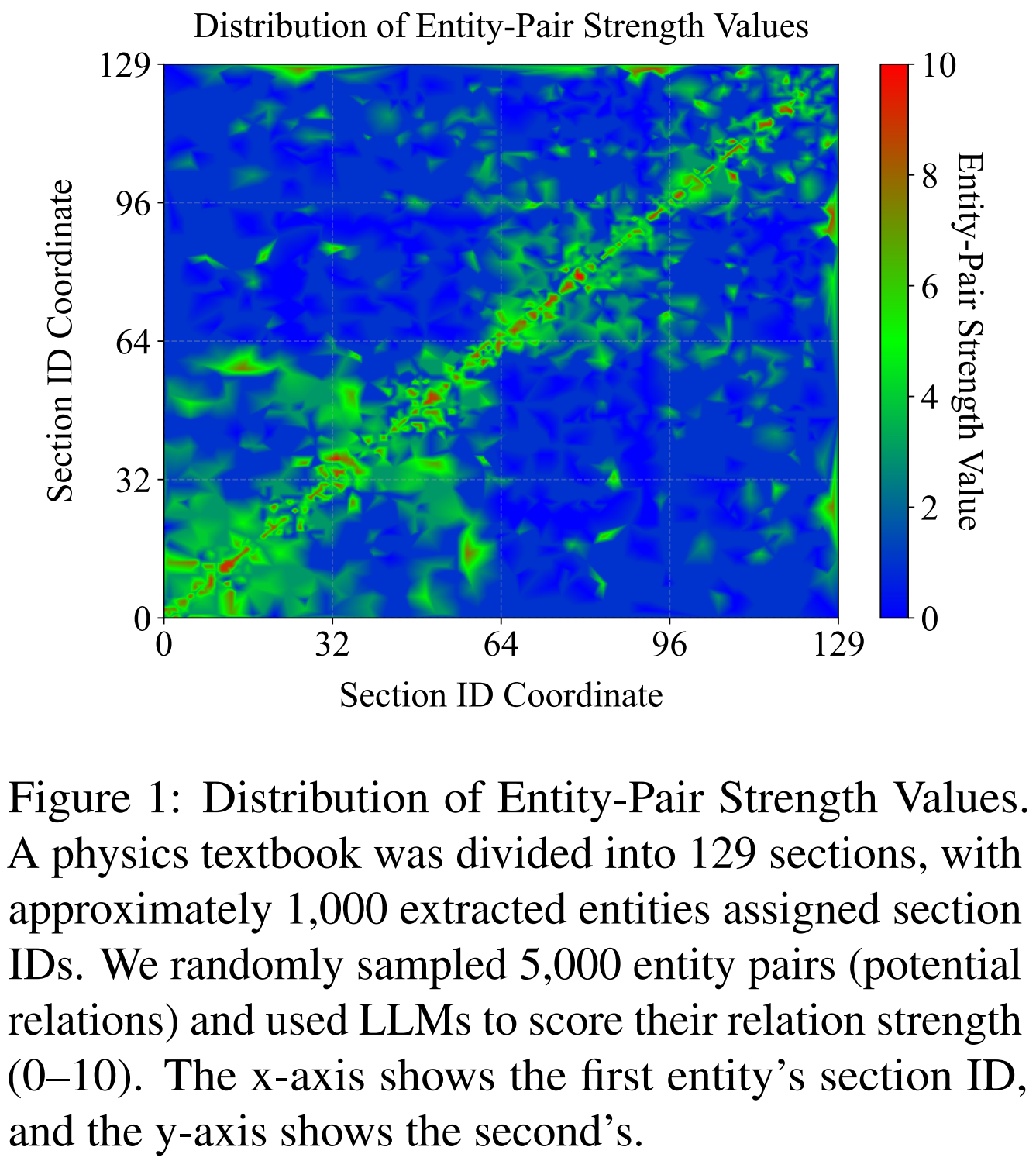
- Figure 1은 교과서의 각 section에 등장하는 entity 간의 관계성 점수(strength score)를 시각화한 결과
- 자기 자신에 대한 관계성 점수가 가장 높게 나타나며
- 주변 section의 entity와의 관계성 점수가 그 다음으로 높게 나타나는 경향을 확인할 수 있음
해결책: Tree-KG
- Tree-KG는 이러한 문제를 해결하기 위해 아래 두 단계 접근 방식을 사용
- 초기 구축 (뼈대 만들기)
- 먼저 교과서나 논문처럼 목차가 있는 구조화된 텍스트를 분석
- 대형언어모델(LLMs)을 활용하여 이 목차 구조를 그대로 따라 트리(Tree) 형태의 기본 지식 그래프를 구축
- 이는 마치 건물의 뼈대를 세우는 skeleton 구축 과정과 동일
- 반복적 확장 (살 붙이기)
- 기본 뼈대가 만들어지면, 미리 정의된 유연한 규칙(operator)을 통해 숨겨진 관계를 찾아내어 그래프를 점진적으로 확장
- 예를 들어, 다른 챕터에 있지만 서로 관련 있는 개념들을 찾아 연결하는 식
- 이를 통해 뼈대에 살을 붙여 풍성하고 완성도 높은 지식 그래프를 구축
- 초기 구축 (뼈대 만들기)
주요 결과 및 장점
- 뛰어난 성능
- 실험 결과, Tree-KG는 기존 다른 방법들보다 월등한 성능을 보임
- F1 점수가 2위 그룹보다 12~16% 더 높았음
- 높은 정보 추출 품질
- 소스 텍스트에서 정보를 정확하게 추출하는 능력이 뛰어남
- 특정 데이터셋에서는 0.81이라는 높은 F1 점수를 기록
- 구조적 우수성
- 교과서 구조를 기반으로 하여 생성한 KG는 논리적으로 잘 정렬되어 있음
- 특정 전문 분야의 지식을 효과적으로 표현
- 비용 효율성
- 더 적은 LLM 토큰(비용)을 사용하면서도 강력한 결과를 도출
- 비용 효율적이고 자원 친화적인 구축이 가능
2. Related Work
1. 전통적 방식: 규칙 기반 및 지도 학습
- 규칙 기반 (Rule-based)
- “A는 B의 수도이다”와 같은 문법적, 의미적 규칙을 사전에 정의하여 지식을 추출
- 정확도는 높지만, 규칙을 만들기 어렵고 새로운 형태의 문장에는 적용하기 힘든 단점이 있음
- 지도 학습 (Supervised)
- 정답이 표시된 대규모 데이터셋을 모델에 학습시켜 관계 추출 패턴을 익히게 만듦
- 성능은 좋지만, 고품질의 학습 데이터를 만드는 데 많은 비용과 시간이 들고 확장성이 부족
2. LLM 기반 방식: 더 똑똑하고 유연한 접근
- 온톨로지 기반 (Ontology-based)
- 위키피디아처럼 이미 잘 구축된 지식 체계(온톨로지)를 기반으로
- LLM을 활용해 새로운 텍스트에서 관계 후보를 생성하고 기존 지식에 연결
- 기존 지식 체계의 품질에 성능이 크게 좌우됨
- 미세 조정 (Fine-Tuning)
- 특정 데이터셋에 맞게 LLM을 추가로 학습시켜 관계 추출 성능을 극대화
- 특정 환경에서는 높은 성능을 보이나, 학습하지 않은 새로운 데이터나 너무 많은 종류의 관계를 처리하는 데는 어려움이 존재
- 제로샷/퓨샷 학습 (Zero- & Few-shot Learning)
- 별도의 학습 데이터 없이(제로샷) 또는 아주 적은 예시만으로(퓨샷) LLM에게 지시하여 지식을 추출
- 데이터 준비 부담이 적지만, 때때로 개념을 정확히 구분하지 못하거나 계산 비용이 많이 들 수 있음
- 지식 집약적 도메인 특화
- 수학(MathGraph)이나 교육처럼 특정 전문 분야에 맞춰 LLM을 전문가처럼 활용하는 시스템
- 높은 정확도를 보이지만, 해당 분야에만 적용할 수 있어 범용성이 떨어짐
결론: 균형 잡힌 프레임워크의 필요성
- 결론적으로, 지식 집약적 분야를 위한 효과적인 KG 구축 프레임워크는 자동화, 정확성, 적응성, 지식 통합 능력 사이에서 균형을 맞추어야 함
- 이 글의 저자들이 제안하는 Tree-KG는 바로 이러한 균형을 목표로 하는 프레임워크
3. Methodology
3.1 Definitions
3.1.1 Tree-like Hierarchical Graph
- Tree-KG가 생성하는 지식 그래프의 기본 구조
-
트리 자료구조와 같이 여러 계층으로 구성
- 정점 (Node, V): 그래프의 각 개념(엔티티)은 특정 계층($V_1, V_2, …, V_k$)에 속함
- 정점 집합 $V$는 $k$ 레이어로 분할됨 (The node set $V$ is partitioned into $k$ layers)
- $V = V_1 \cup V_2 \cup … \cup V_k$
- 각 부분 집합 $V_i$는 특정 레이어와 대응 (where each subset $V_i$ corresponds to a specific layer)
- $V_i \cup V_j = \emptyset$ for $\forall (i \neq j)$
- 정점 집합 $V$는 $k$ 레이어로 분할됨 (The node set $V$ is partitioned into $k$ layers)
- 간선 (Edge, E): 두 종류의 간선이 존재
- 수직 간선 (Vertical Edges, $E_1$)
- 서로 다른 계층의 노드를 연결
- e.g., ‘물리학’ 챕터 → ‘전자기학’ 섹션
- 위 간선들은 전체적으로 트리 구조를 형성
- 수평 간선 (Horizontal Edges, $E_2$)
- 동일한 계층 내의 정점을 연결
- e.g., ‘전하’ 개념 ↔ ‘전자’ 개념
- 수직 간선 (Vertical Edges, $E_1$)
- 수직 간선 (Verical Edges, $E_1$)
- 서로 다른 계층 간의 연결을 구성
- 인접한 계층 간에만 연결을 구성 (the edge can only connect adjacent layers)
- For each edge $(u, v) \in E_1$, if $u \in V_i$ and $v \in V_j$, then $\vert i-j \vert = 1$
- 수평 간선 (Horizontal Edges, $E_2$)
- 서로 같은 계층 간의 연결을 구성
- For each edge $(u, v) \in E_2$, if $u, v \in V_i$, then the edge connects nodes within the same layer $V_i$
3.1.2 KG Schema
-
지식 그래프를 구성하는 정점과 간선의 구체적인 설계 명세
- 정점 (Node)의 속성
- 이름 (name): 정점의 고유한 이름 (e.g., ‘Electric Charge’)
- 설명 (description): 텍스트에서 추출한 개념 설명
- 관계 (relations): 해당 정점에 연결된 간선 정보
- 간선 (Edge)의 종류
- 수직 간선
has_subsection(상위섹션-하위섹션),has_entity(섹션-개념),has_subordinate(핵심개념-비핵심개념) 등 계층/소속 관계를 표현
- 수평 간선
- LLM이 예측한 구체적인 관계(e.g., ‘obey’, ‘has’)와 일반적인 카테고리(
section_related,entity_related)를 결합하의 의미 관계를 표현
- LLM이 예측한 구체적인 관계(e.g., ‘obey’, ‘has’)와 일반적인 카테고리(
- 수직 간선
3.1.3 Adamic-Adar Score
-
두 정점 $(u, v)$가 얼마나 연결될 가능성이 높인지를 공통 이웃(common neighbors)을 기반으로 계산
- 핵심 아이디어
- 단순히 공통 이웃이 많다고 중요한 것이 아님
- 영향력 있는 공통 이웃을 공유하는 것이 더 중요
- 여기서 영향력은 해당 이웃이 얼마나 적은 수의 다른 노드와 연결되어 있는지(희소성)으로 판단
- 수식
- $AA(u,v)=\sum_{w \in N(u) \cap N(v)}{\frac{1}{log(\vert N(w) \vert)}}$
- $N(u)$: Set of neighbors of node $u$ (i.e., 정점 $u$의 이웃 정점)
- $N(v)$: Set of neighbors of node $v$ (i.e., 정점 $v$의 이웃 정점)
- $\vert N(w) \vert$: Degree of node $w$ (i.e., 정점 $w$의 차수)
- AA 점수를 계산할 시에는 그래프 전체를 무방향으로 간주
- $AA(u,v)=\sum_{w \in N(u) \cap N(v)}{\frac{1}{log(\vert N(w) \vert)}}$
3.1.4 Number of Common Ancestors
- 두 정점$(u, v)$가 계층적으로 얼마나 가까운지를 측정하는 지표
- 계산 방식
- 각 정점에서 수직 간선을 따라 최상위 계층까지 올라가는 모든 경로를 찾음 (Lineage Path)
- 두 정점의 경로 간에 겹치는 조상 정점의 최대 개수를 계산 (Common Ancestors)
- 공통 조상이 많을 수록 두 정점은 구조적으로 더 가깝다고 간주
- Lineage Path
- 시작점: 정점 $u$, 정점 $v$
- 경로 탐색: 수직 간선 (Vertical Edges)만을 따라 위쪽(upwards) 계층으로만 이동
- 종료점: 최상위 계층 (the first layer)에 도달하면 중단
- $P_u$, $P_v$의 정의
- $P_u$: 정점 $u$에서 시작해 최상위 계층까지 도달하는 모든 가능한 수직 경로들의 집합
- $P_v$: 정점 $v$에서 시작해 최상위 계층까지 도달하는 모든 가능한 수직 경로들의 집합
- Common Ancestors
- 두 정점 $u$와 $v$가 얼마나 가까운 친척 관계인지를 계산
-
앞서 구한 ‘조상 경로 집합’ $P_u$와 $P_v$를 사용
- $CA(u,v)=max(\vert P_u^{(i)} \cap P_v^{(j)} \vert)$
- 모든 경로 조합 생성
- $P_u$ 경로 집합 중 하나($P_u^{(i)}$)와 $P_v$ 경로 집합 중 하나($P_v^{(j)}$)를 짝지어 쌍(pair)을 생성
- 가능한 모든 조합에 대하여 수행
- number of combinations: $\binom{\vert P_u \vert}{\vert P_v \vert}$
- 공통 조상 계산 (Intersection)
- 짝지어진 두 경로 ($P_u^{(i)}$, $P_v^{(j)}$)에 공통으로 포함된 조상 노드가 몇 개인지 계산
- 최댓값 선택 (Max)
- 1~2단계에서 계산된 여러 개의 ‘공통 조상 수’ 중에서 가장 큰 값 하나를 선택.
- 이 값이 최종적인 공통 조상수 $CA(u, v)$
- Common Ancestors, 왜 최댓값(max)을 사용하는가?
- 하나의 개념(정점)은 여러 상위 카테고리에 동시에 속할 수 있음
- 예를 들어, 레이저(Laser)라는 개념을 생각해보자
- 레이저(Laser)는 광학(Optics)의 하위 개념일 수 있음 (경로 1)
- 레이저(Laser)는 전기 공학(Electrical Engineering)의 하위 개념일 수 있음 (경로 2)
- 이제 레이저($u$)와 광자($v$)의 관계를 찾는다고 가정해보자
- $P_u^{(1)}$: 레이저 $\rightarrow$ 광학 $\rightarrow$ 물리학 $\rightarrow$ 과학
- $P_u^{(2)}$: 레이저 $\rightarrow$ 전기 공학 $\rightarrow$ 공학 $\rightarrow$ 과학
- $P_v^{(1)}$: 광자 $\rightarrow$ 양자 역학 $\rightarrow$ 물리학 $\rightarrow$ 과학
- 모든 경로의 조합을 생성한 후 공통 조상을 계산해보자
- $(P_u^{(1)}, P_v^{(1)})$: {‘물리학’, ‘과학’} $\rightarrow$ 공통 조상 2개
- $(P_u^{(2)}, P_v^{(1)})$: {‘과학’} $\rightarrow$ 공통 조상 1개
- ❌ 최솟값(min)
- min(2, 1) = 1
- 문제점: ‘레이저’가 ‘공학’에도 속한다는 이유만으로, ‘광자’와의 명백한 ‘물리학’적 연결고리가 무시
- ❌ 평균값(avg)
- avg(2, 1) = 1.5
- 문제점: 강한 연결(2)과 약한 연결(1)이 섞이면서, “둘은 어중간하게 관련 있다”라는 애매한 결론
- 👍 최댓값(max)
- max(2, 1) = 2
- 의미: “이 두 개념은 ‘물리학’이라는 매우 강력한 공통분모를 가지고 있구나!”라는 사실을 찾아냄
- 결론적으로, 여러 연결 경로 중에서 가장 의미 있고, 가깝고, 강력한 관계를 하나라도 찾아내기 위함
- 두 개념이 단 하나의 강력한 상관 관계가 있으면, 그 둘을 ‘관련 있다’라고 말할 수 있음
3.2 Knowledge Graph Construction & Expansion
- ‘Tree-KG’ 프레임워크의 작동 방식은 아래의 두 단계로 구성
- Phase 1: 초기 구축 (뼈대 만들기)
- 교과서처럼 계층 구조가 명확한 텍스트를 활용
- 지식 그래프의 기본 뼈대를 구축
- Phase 2: 반복적 확장 (살 붙이고 다듬기)
- 초기 골격(skeleton) 그래프는 교과서에 명시된 관계만 가지고 있음
- 이 단계에서는 숨겨진(latent) 관계들을 포착해 그래프를 더 풍부하게 구성
- Phase 1: 초기 구축 (뼈대 만들기)
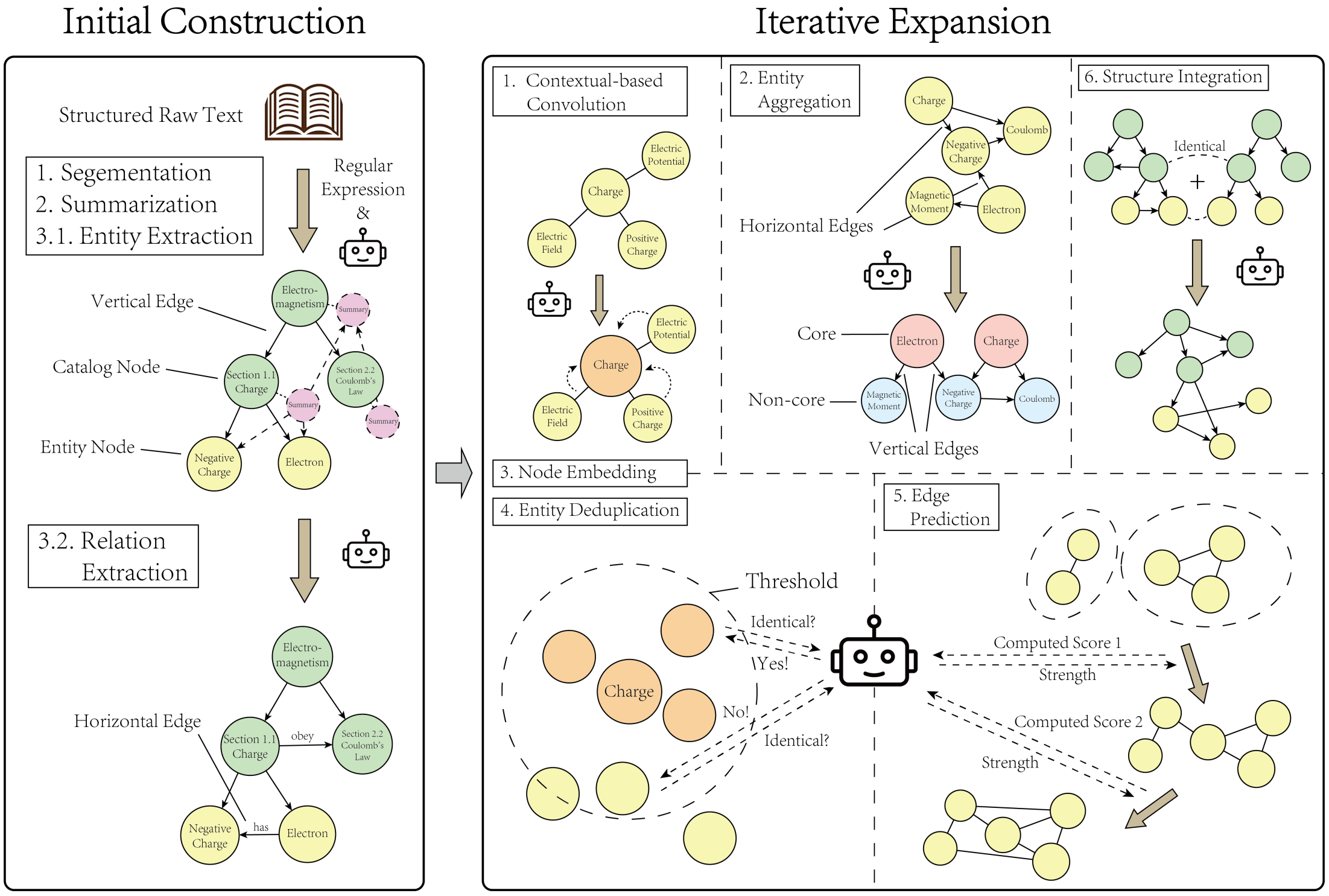
3.3 Phase 1: Initial Construction, Skeleton Construction
- 도메인 코퍼스(즉, 계층적으로 구조화된 교과서)에서 지식 그래프의 기본 골격(skeleton) 추출
- 해당 지식 그래프(KG)는 해당 도메인을 하향식으로 표현
- ‘챕터-섹션-엔티티’와 같은 관계를 포착
- 제안 논문은 위 구조를 활용하여 tree-like hierarchical graph를 구축
3.3.1 Text Segmentation
- 정규 표현식(regular expression, regex)을 사용해 교과서의 ‘1. 장’, ‘1.1 절’, ‘1.1.1 소절’과 같은 제목 형식을 자동으로 인식
- 식별한 목차(Table Of Contents, TOC)는 그대로 그래프의 계층적 ‘목차 정점’으로 사용
has_subsection(하위 섹션을 가짐)이라는 수직 간선으로 연결- e.g., [책] $\rightarrow$ [1. 전자기학] $\rightarrow$ [1.1 전하]
3.3.2 Bottom-Up Summerization
- 가장 말단 정점(e.g., ‘1.1.1 소절’)의 본문 텍스트로부터 LLM을 사용해 요약문 생성
- 그다음, 하위 정점들의 요약문을 합쳐서 상위 정점(e.g., ‘1.1 절’, ‘1장’)의 요약문 생성
- 이러한 상향식(Bottom-up) 방식은 상위 챕터의 요약이 하위 정점의 세부 내용을 잘 반영하도록 보장
3.3.3 Entity and Relation Extraction
- LLM이 다시 한번 요약된 텍스트를 분석하여 핵심 개념(엔티티)와 그들 사이의 관계를 추출
- 엔티티 추출
- 요약문에서 ‘전하(Electric Charge)’, ‘전자(Electron)’같은 핵심 엔티티(개념)을 추출
- 간선 생성
- 수직 간선:
has_entity(개념을 가짐) 간선으로 목차 정점과 엔티티 정점을 연결 - 수평 간선:
entity_related(개념 간 관계) 간선으로 엔티티 간의 관계를 연결 (e.g., [전자] $\rightarrow$has[음전하])
- 수직 간선:
3.4 Phase 2: Iterative Expansion
- Phase 1에서 구성한 명시적인 KG는 견고한 골격을 제공
-
그러나, 도메인 내에서 잠재적이거나 암묵적인 관계를 놓칠 수 있음
-
Phase 2: Iterative Expansion는 텍스트와 구조적 맥락을 통합하여 엔티티 간의 숨겨진 관계를 포착
- 이 단계에서는 ‘문맥 기반 컨볼루션’, ‘엔티티 집계’, ‘노드 임베딩’, ‘엔티티 중복 제거’, ‘간선 예측’, ‘구조 통합’을 포함한 미리 정의된 action set을 수행
- 문맥 기반 컨볼루션: contextual-based convolution (conv)
- 엔티티 집계: entity aggregation (aggr)
- 정점 임베딩: node embedding (embed)
- 엔티티 중복 제거: entity deduplication (dedup)
- 간선 예측: edge prediction (pred)
- 구조 통합: structure integration (merge)
3.4.1 Contextual-based Convolution
-
그래프에 있는 각 엔티티(정점)의 ‘설명(description)’을 더 풍부하고 정확하게 업그레이드하는 과정
- 핵심 아이디어: “주변을 보고 나를 파악한다”
- 전통적인 GCN (Graph Convolution Neural Network)이 이웃 정점의 피쳐 벡터를 종합(aggregation)하여 현재 정점의 피쳐 벡터를 업데이트하는 것에서 영감을 얻음
- 하지만, Tree-KG는 벡터 대신 텍스트 설명, 행렬 연산 대신 LLM을 사용
- 작동 방식: LLM이 ‘종합 리포트’ 작성
- LLM은 특정 엔티티 $v$에 대해 다음 두 가지 정보를 입력받음
- $h_v$: $v$ 자신의 기존 설명문 (e.g., “전하: 물체가 띠는 전기적 성질”)
- ${ h_u }$: $v$의 모든 이웃 노드 $N(v)$들의 설명문 (e.g., “전기장: 전하 주변에 생기는 힘”, “양전하: …”, “음전하: …”, …)
- LLM은 이 정보들을 모두 종합하여 $v$에 대한 새로운, 더 풍부한 설명(i.e., $h_v^{(\text{new})}$)이 담긴 리포트를 생성
- 이 리포트에는 다음의 내용을 포함
- $v$의 명확한 재정의
- 이웃 정점($N(v)$)들을 고려한 $v$의 상세한 문맥 정보
- 로컬 부분 그래프 내에서 $v$가 맡는 역할
- $h_v^{(\text{new})} = conv(h_v, {h_u : u \in N(v)})$
- $h_v^{(\text{new})}$ (새 설명) = LLM이 conv(합성곱 작업)을 수행한 결과물
- $h_v$ (기존 설명) + ${ h_u }$ (이웃 정점들의 설명)
- LLM은 특정 엔티티 $v$에 대해 다음 두 가지 정보를 입력받음
- 결과 예시
- 위 과정을 거치면 ‘전하’의 설명은 “물체가 띠는 전기적 성질에서”
- “전기장을 생성하고 양전하와 음전하로 구분되며…“와 같이 주변 개념과의 관계가 반영된 설명으로 업데이트
- 논문 실험에 따르면, 이 작업은 여러 번 반복할 필요 없이 단 한 번만 수행해도 충분
3.4.2 Entity Aggregation
- 그래프를 더 깔끔하게 정리하고, 핵심 개념 중심으로 재편
- 개념들을 핵심(core)과 비핵심(non-core)이라는 두 가지 역할로 분류
- $r \in {\text{core}, \text{non-core}}$
- 작동 방식
- 역할 할당
- LLM이 각 엔티티의 설명(description)을 읽음
- 그 중요도에 따라
core(e.g., ‘전하’)또는non-core(e.g., ‘마찰전기 효과’) 역할을 부여
- 관계 재정의
- ‘전하’(핵심)와 ‘마찰전기 효과’(비핵심)가 원래 수평 간선(동등한 관계)으로 연결되어 있었다면, 이 연결을 수직 간선(상하 관계)로 변경
- 계층 생성
- ‘마찰전기 효과’는 ‘전하’의 하위 개념(child), 이 관계는
has_subordinate(하위 종속 개념을 가짐)라는 간선으로 표현 - 기존: [전하] $\leftrightarrow$ [마찰전기 효과]
- 변경: [전하] $\rightarrow$ has_subordinate $\rightarrow$ [마찰전기 효과]
- ‘마찰전기 효과’는 ‘전하’의 하위 개념(child), 이 관계는
- 역할 할당
- 최종 결과 및 목적
- 그래프 구조 단순화: 이 작업을 통해 최하위의 엔티티 계층을 ‘핵심 엔티티 층(Core entity layer)’와 그 아래 ‘비핵심 엔티티 층(Non-core entity layer)’이라는 명확한 2단 구조로 정리
- 효율성 증대: 복잡한 수평 관계망이 단순한 트리 구조로 바뀌어, 나중에 정보를 검색(질의)할 때 속도가 빨라지고 분석이 쉬워짐
- 현실 반영: 실세계의 지식 구조처럼
- 중요한 중심 개념(e.g., 전하)이 하위 구조(e.g., 마찰전기 효과)를 파생하는 구조를 반영
- 덜 중요한 개념(e.g., 마찰전기 효과)을 중요한 중심 개념(e.g., 전하)에 포함되는 관계를 반영
3.4.3 Node Embedding
-
각 정점(개념)의 텍스트 설명을 벡터로 임베딩하는 과정
- 작동 방식
- 텍스트 $\rightarrow$ 벡터
- 각 노드의 (이전 conv 단계에서 풍부해진) 설명문을 $\text{embed}$ 함수를 통해 $d$차원의 벡터 $z$로 변환
- $z = \text{embed}(\text{“node’s text”})$
- 정규화 (Normalization)
- 벡터 $z$를 길이가 1인 단위 벡터(${\vert z \vert}_2 = 1$)로 정규화
- 모든 벡터가 동일한 ‘크기’를 갖게 되어, 오직 ‘방향’만으로 의미를 비교할 수 있음
- 거리 계산
- 두 정점 $v_i$와 $v_j$가 의미적으로 얼마나 다른지(거리)는 L2 norm (유클리드 거리)을 활용하여 계산
- i.e., ${\vert z_i - z_j \vert}_2$를 사용하여 계산
- 텍스트 $\rightarrow$ 벡터
- 최종 결과 및 목적
- $embed$ 단계는 새로운 엔티티나 관계를 예측(predict)하는 것이 아님
- 생성한 벡터를 다른 연산자(operator)나 최종 시스템이 “더 쉽게 일할 수 있도록” 도와주는 핵심 도구역할을 수행
- $dedup$ (중복 제거) 연산자가 “의미가 비슷한” 정점을 찾을 때 계산한 벡터 거리를 사용
- $pred$ (간선 예측) 연산자가 “두 정점이 의미적으로 얼마나 유사한지” (i.e., $cos(z_u, z_v)$)를 계산할 때 이 벡터를 사용
- RAG (검색 증강 생성) 같은 최종 시스템에서, 사용자의 질의를 벡터로 변환한 뒤, 그래프에서 가장 가까운(유사한) 개념 정점을 계산한 벡터를 활용해 빠르고 정확하게 찾을 수 있음
3.4.4 Entity Deduplication
- 이름만 다르고 의미는 같은 중복된 엔티티(개념)들을 찾아서 하나로 합치는 과정
-
예를 들어, “Electric Charge”와 “Charge”라는 노드가 따로따로 만들어졌다면, 이 둘이 사실상 같은 개념임을 파악하고 병합
- 작동 절차
- 준비 (Setup)
- 각 엔티티($v$)의 임베딩 벡터($z$)와 역할(r)(e.g.,
core/non-core)를 미리 계산 - 처음에는 모든 엔티티가 “나는 나 자신과만 같다”는 별개의 그룹(equivalence class)에 속해 있다고 가정
- 각 엔티티($v$)의 임베딩 벡터($z$)와 역할(r)(e.g.,
- 유사 후보 검색 (Candidate Search)
- FAISS 벡터 검색이라는 고속 검색 기술을 사용
- 각 엔티티($v$)마다, 임베딩 벡터 공간에서 가장 가까운 이웃 20개(v’)를 빠르게 찾아냄
- 1차 필터링 (Filtering)
- 이 20개의 후보($v$, $v’$) 중에서 다음 두 가지 조건을 동시에 만족하는 쌍만 남김
- 거리 조건: 두 벡터 사이의 거리가 미리 정해둔 기준값($\text{threshold}_{\text{dedup}}$)보다 가까워야 한다
- 역할 조건: 두 엔티티의 역할($r_v$, $r_{v’}$)이
core이면core,non-core이면non-core로 서로 같아야 한다
- 이 20개의 후보($v$, $v’$) 중에서 다음 두 가지 조건을 동시에 만족하는 쌍만 남김
- 최종 검증 (LLM Verification)
- 1차 필터링을 통과한 후보 쌍들을 거리가 가까운 순서대로 정렬
- LLM에게 “이 두 엔티티$(v, v’)$가 정말로 같은 의미의 개념인가?”라고 질문 (벡터 거리가 가깝다고 무조건 같은 개념이 아님. ‘사과’와 ‘배’는 가깝지만 같지는 않음)
- 병합 (Merging)
- 만약 LLM이 “그렇다, 둘은 같다”라고 판정하면, Union-Find(합집합 찾기) 알고리즘을 사용해 두 엔티티가 속한 그룹을 하나의 그룹으로 병합
- 이 과정을 반복하면, ‘Electric Charge’, ‘Charge’, ‘전하’가 모두 “같은 그룹”으로 묶임
- 준비 (Setup)
3.4.5 Edge Prediction
- 그래프에 누락된 관계(간선)을 예측하여 추가하는 과정
-
지식 그래프를 완성하는 핵심 과정
- 핵심 아이디어: “관계가 있을 법한” 엔티티는?
- 해당 도메인의 전문가 검증을 통해, 두 엔티티($u$, $v$)가 아래 세 조건을 만족할 때 연결될 가능성이 높다는 것을 확인
- 의미가 비슷하다 (e.g., ‘전압’과 ‘기전력’)
- 공통의 이웃이 많다 (e.g., ‘A’와 ‘B’가 둘 다 ‘C’와 연결)
- 공통의 조상이 많다 (e.g., 둘 다 ‘물리학’ 챕터의 하위 개념)
- 해당 도메인의 전문가 검증을 통해, 두 엔티티($u$, $v$)가 아래 세 조건을 만족할 때 연결될 가능성이 높다는 것을 확인
3.4.6 Structure Integration
- 새로운 텍스트나 데이터가 발견되었을 때, 이를 기존에 만들어둔 지식 그래프(KG)에 합치는 과정
- 지식 집약적 분야는 끊임없이 발전하기 때문에, 지식 그래프도 점진적으로(incrementally) 업데이트 될 수 있어야함
-
merge연산자는 이 통합 과정을 담당 - 구조가 없는 텍스트 (Unstructured Texts)
- 독립된 미니 그래프 생성
- 새 텍스트($G’$)을 가져와서
conv,aggr,embed등 앞서 설명한 연산자를 적용- 일단 그 자체로 작은 지식 그래프(subgraph)를 생성
- 겹치는 개념 병합 (Merge Overlaps)
- 새 그래프($G’$)의 노드들과 기존 그래프($G$)의 노드들의 임베딩 벡터를 비교
- 벡터가 매우 유사하면 (즉, 같은 개념이라면) 두 노드를 하나로 합침
- 위 과정에서, 기존 노드가 가지고 있던 ‘섹션 목차 라벨’(e.g., “3.1장 소속”) 정보는 그대로 유지
- 새로운 개념 연결 (Link News Components)
- 일부만 겹칠 때: 새 노드가 기존 컴포넌트에 병합되면, Graph Coloring 알고리즘을 활용해 라벨을 붙임
- 불필요하게 다른 섹션과 간선이 생기는 것을 최소화
- 가장 관련 있는 섹션에 소속되도록 유도
서로 관련이 적은 섹션 간에는 간선이 적을 것띠리서, 서로 간선이 적은 노드 집합 간에는 동일한 color(label)을 붙일 가능성이 클 것같은 색을 사용하는 노드가 많은 서브그래프(섹션)에는 간선을 최대한 생성하지 않겠다는 의미로 개인적으로 해석- 완전히 새로울 때: 새 그래프($G’$)가 기존 그래프($G$)와 전혀 겹치지 않는 ‘고립된 섬’이라면, $G’$의 중심 임베딩 벡터(i.e., channel-wise 평균 벡터)를 계산
- 그 다음, 기존 그래프의 모든 섹션 ‘섹션 목차 노드’ 중, 유사도가 가장 큰 섹션에 이 섬을 통째로 연결
- 독립된 미니 그래프 생성
- 구조가 있는 텍스트 (Structured Texts)
- 계층 구조 우선 병합
- 새 텍스트에도 목차(계층 구조)가 존재
- 우선, 목차 트리(catalog tree)를 생성
- 이후, 기존 목차 트리와 재귀적으로 병합
- 병합 기준: 임베딩 유사도 혹은 고유한 식별자(unique identifiers)
- 겹치는 개념 병합
- 구조가 없는 텍스트(Unstructured Texts)와 동일한 방식으로 통합 연산 수행
- 계층 구조 우선 병합
- 결론
merge연산자는 새로운 정보가 들어왔을 때, 기존 그래프의 논리적 계층 구조를 보존하면서- 새로운 지식을 효과적으로 확장(통합)할 수 있게 해줌
4. Experiments
4.1 Experimental Setup
4.1.1 Datasets
- 데이터 출처 및 규모
- 프로젝트: 저자 연구소의 AI4EDU 프로젝트에서 수집된 자료를 활용
- 구성: 약 69,000개의 전문 자료(교과서, 강의 노트, 학술 논문)로 구성된 대규모 코퍼스
- 범위: 약 100개의 세부 분야에 걸쳐 있으며, 총 995만 개의 지식 포인트(knowledge point)를 포함
- 출처: 연구소 내 다양한 학과에서 자료를 수집, 여러 전문 도메인의 KG를 구축할 수 있는 풍부한 기반을 마련
- 데이터 품질 관리
- 가이드라인 및 교육: 데이터 검토자(annotator)들은 명확한 가이드라인을 받고 훈련을 이수
- 독립적 작업: 여러 명의 조교(TA)가 독립적으로 데이터를 검토 및 분류
- 의견 조율: 의견이 일치하지 않는 부분은 지도교수의 주도하에 합의를 통해 해결
- 신뢰도 검증: 무작위로 샘플을 뽑아 플라이스 카파 (Fleiss’ Kappa)라는 통계적 척도를 사용해 검토자간 일치도(IAA, Inter-Annotator Agreement)를 평가
- 핵심 평가 도메인
- 물리학(Physics), 디지털 전자공학(Digital Electronics), 교육 심리학(Educational Psychology)
- Ground Truth
- Domain-Annotated (전문가 지식 기반)
- 전문가들이 물리학 교과서 뿐 아니라, 해당 분야 전체의 포괄적인 지식을 바탕으로 직접 구축한 “이상적인” 지식 그래프
- Text-Annotated (교과서 기반)
- 전문가들이 오직 제공된 교과서 텍스트만을 기반으로 수동으로 추출하고 구축한 지식그래프
- 모델이 교과서 내용을 얼마나 잘 추출했는지 평가하기 위함
- Appendix-List (부록 목록)
- 교과서 부록에 실린 핵심 지식 포인트 목록을 정답으로 활용
- Domain-Annotated (전문가 지식 기반)
4.1.2 Baseline Methods
- Tree-KG(T)
- 제안 기법
- GraphRAG(G)
- RAG 프레임워크
- 이번 실험에서는 기본적인 추출/요약 기능만 사용
- Tree-KG의 핵심인 반복적 확장, 계층 구조 활용, 추론 기반 정제 기능이 빠져있음
- iText2KG(I)
- 수동으로 스키마(규칙)를 정의
- 반복적 확장이나 정렬 기능이 없음
- LangChain(L)
- 템플릿 기반으로 작동
- 깊이 있는 의미 분석 기능이 없음
- AutoKG(A)
- 멀티 에이전트를 사용
- 특정 전문 도메인의 구조를 잘 반영하지 못할 수 있음
4.1.3 Evaluation Startegies
- (1) Ground Truth
- 물리학(Physics) 도메인에서, 전문가가 직접 만든 3가지 종류의 정답셋을 기준으로 모델이 생성한 KG를 채점
Domain-Annotated: 전문가의 포괄적인 도메인 지식 기반 정답셋Text-Annotated: 전문가가 오직 교과서 텍스트만 보고 추출한 정답셋Appendix-List: 교과서 부록의 핵심 용어 목록
- 물리학(Physics) 도메인에서, 전문가가 직접 만든 3가지 종류의 정답셋을 기준으로 모델이 생성한 KG를 채점
- (2) Mutual Evaluation
- 정답셋이 없는 3개의 도메인에서, 5개 모델이 서로의 생성 결과를 정답으로 삼아 상호 채점
- e.g., Tree-KG가 만든 결과를 기준으로 GraphRAG의 성능을 평가
- (3) LLM-Based Evaluation
- LLM에게 몇 가지 예시(few-shot)을 제시
- 생성된 KG의 품질(정확성, 일관성)을 평가하도록 지시
4.1.4 Metrics
- 정답(Ground Truth)이 있는 경우
- 제안 기법으로 생성한 KG: $G=(V,E)$
- 전문가가 생성한 KG(Ground Truth): $G_{\text{gt}}=(V_{\text{gt}}, E_{\text{gt}})$
- (a) Entity Recall (ER, 재현율)
- $G_{gt}$의 정답 엔티티가 모델이 생성한 $G$에 몇 개 포함되어 있는가?
- $G_{gt}$의 $V_{gt}$에 대해
- $G$의 모든 엔티티 중에서 $V_{gt}$와 임베딩 벡터가 가장 유사한 상위 5개를 추출
- LLM이 그 5개 후보에 대해 $V_{gt}$와 의미적으로 동일한 것이 있는지 판단하여 최종 매핑을 수행
- 위 과정을 $G_{gt}$의 모든 엔티티에 대해 반복한 뒤 ER을 계산
- $G_{gt}$의 정답 엔티티가 모델이 생성한 $G$에 몇 개 포함되어 있는가?
- (b) Precision (PC, 정밀도)
- 모델이 생성한 $G$에 포함된 엔티티가 $G_{gt}$의 정답 엔티티에 몇 개 존재하는가?
- $G$의 $V$에 대해
- $G_{gt}$의 모든 엔티티 중에서 $V$와 임베딩 벡터가 가장 유사한 상위 5개를 추출
- LLM이 그 5개 후보에 대해 $V$와 의미적으로 동일한 것이 있는지 판단하여 최종 매핑을 수행
- 위 과정을 $G$의 모든 엔티티에 대해 반복한 뒤 PC를 계산
- 모델이 생성한 $G$에 포함된 엔티티가 $G_{gt}$의 정답 엔티티에 몇 개 존재하는가?
- (c) F1 Score (F1)
- ER과 PC의 조화평균
- (d) Mapping-based Edge Connectivity (MEC, 연결성)
- $G_{gt}$의 간선이 $G$에도 경로로 연결되어 있는지 확인
- 직접 연결이 아니어도 됨
- $G_{gt}$의 간선 $(u,v)$에 대해 $G$에서 $u$에서 $v$로 이동하는 경로가 존재하는지 검사
- 즉, 두 개념의 연결성을 유지하는지 검사
- (e) Mapping-based Edge Distance (MED, 거리)
- $G_{gt}$에서는 1-hop 이웃인 $(u,v)$ 쌍에 대해 $G$에서의 거리를 측정
- $d_G(u,v)=\text{shortest path distance between } u,v \text{ in } G$
- $\overline{d_G}=\text{average shortes path distance in } G$
- i.e., $\overline{d_G}=\frac{1}{\vert E \vert}\sum_{(u,v) \in E} d_G(u,v)$
- 정답(Ground Truth)이 없는 경우
- 제안 기법으로 생성한 KG: $G=(V,E)$
- $G$를 LLMs를 활용하여 평가
- for each entity
- specificity: 0 or 1
- completeness: 0 to 10
- strength: 0 to 10
- (f) Entity Specificity (ES, 엔티티 전문성)
- specificity: 엔티티가 해당 도메인과 얼마나 관련이 깊은가?
- LLMs를 활용하여 0점 혹은 1점으로 평가
- $G$ 내의 모든 엔티티(정점)에 대한 specificity의 평균
- (g) Entity Completeness (EC, 엔티티 완성도)
- 엔티티의 설명이 얼마나 충실한가?
- LLMs를 활용하여 0점에서 10점 사이로 평가
- $G$ 내의 모든 엔티티(정점)에 대한 completeness의 평균
- (h) Relation Strength (RS, 관계 강도)
- 두 엔티티 간의 관계(간선)가 얼마나 가깝고 명료한가?
- LLMs를 활용하여 0점에서 10점 사이로 평가
- Entity Scoring Example
- Role: You are an educational knowledge graph expert skilled in evaluating entity extraction quality. - Task: Given a knowledge domain, chapter overview, and extracted entities, score each entity's specificity and description completeness. - Constraints - Score two metrics (0 or 1, 0-10): * Specificity: 0=irrelevant, 1=highly relevant * Completeness: 1=incomplete, 5=basic, 9=comprehensive - Output must be a valid JSON list. - Output Template [ { "id": "Entity ID", "specificity": 0 or 1, "completency": 0-10 } ]
4.2 Main Results
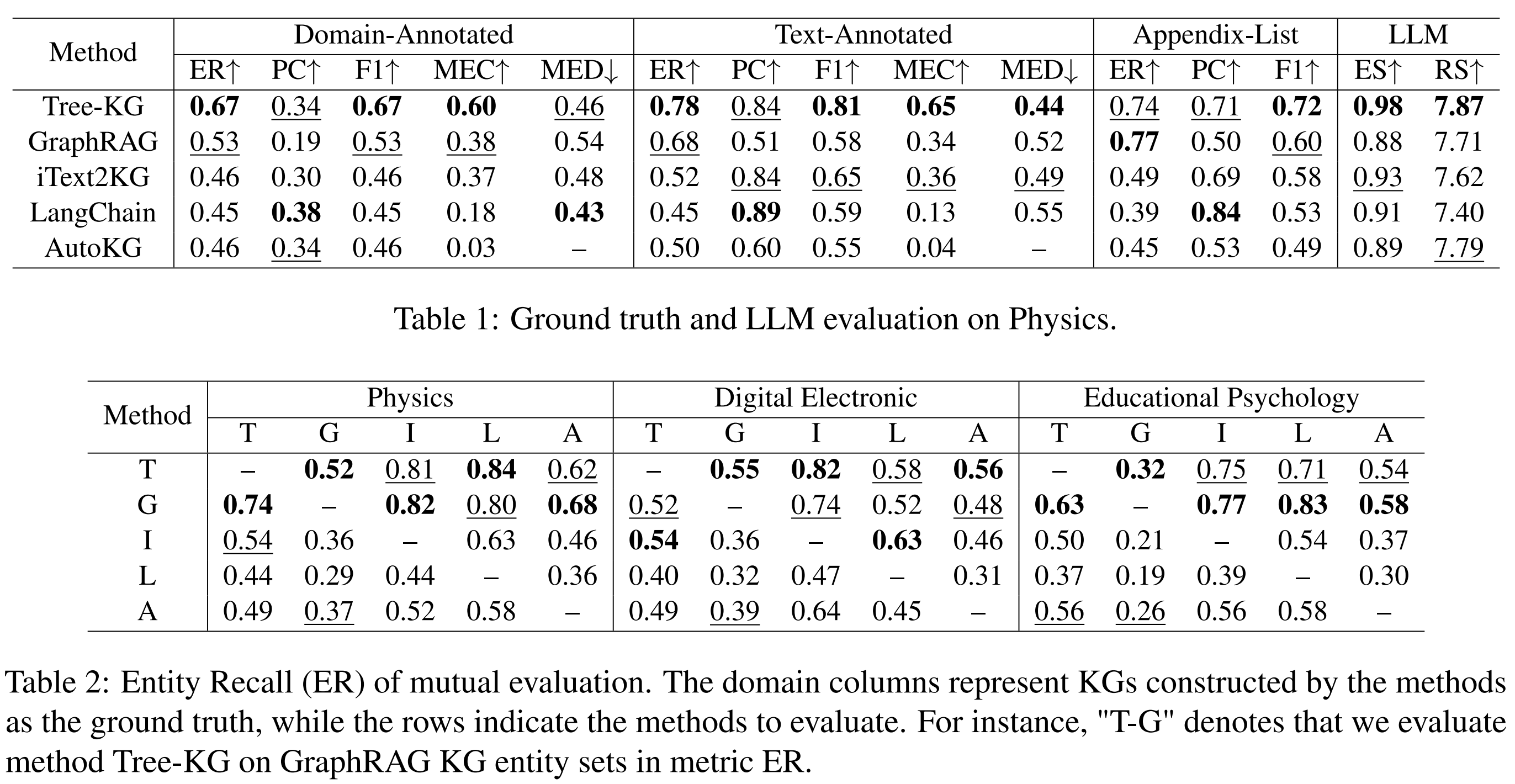
4.2.1 Sufficiency & Balance
Tree-KG는 도메인 전문 교과서 내에서 ‘엔티티’를 찾아내고 그 정확도를 유지하는 데 뛰어난 균형을 보여줌
- 재현율(ER) 우위
- Ground Truth와 Mutual Evaluation 모두에서 GraphRAG와 비슷하거나 이를 상회하는 가장 높은 수준의 재현율을 기록
- 특히 Domain-Annotated 데이터에서 2위 모델보다 14% 높은 성능을 기록
- 가장 높은 F1 점수
- 정밀도(PC)와 재현율(ER)의 조화평균을 나타내는 F1 점수가 2위 모델보다 12~16% 더 높음
- 텍스트 추출 품질
- Text-Annotated 데이터에서 0.81이라는 높은 F1 점수를 달성
- 원문에서 고품질 정보를 추출하는 능력을 입증
4.2.2 Structural Alignment
지식 간의 관계(간선)를 얼마나 논리적이고 촘촘하게 연결했는지를 보여주는 지표에서 경쟁 모델들을 압도
- 높은 연결성(MEC, Mapping-based Edge Connectivity)
- Ground Truth와 비교했을 때, 개념 간의 연결 관계를 보존하는 능력(MEC)이 타 모델 대비 1.6배에서 최대 20배까지 높음
- 짧은 논리적 거리(MED, Mapping-based Edge Distance)
- Ground Truth에서 가깝게 정의된 개념들을 실제 그래프상에서도 가깝게 배치하는 능력(MED)이 가장 우수
- 타 모델의 0.8 ~ 1.1배 수준
- 원래 지식의 구조를 가장 잘 복제해냄
4.2.3 Domain Expertise
LLM을 활용한 질적 평가에서도 Tree-KG는 가장 전문적인 결과를 도출
- 엔티티 전문성(ES, Entity Specificity)
- 추출된 개념들이 해당 도메인에 얼마나 특화되어 있는지를 측정하는 지표에서 가장 앞섬
- 관계 강도(RS, Relation Strength)
- 개념들을 잇는 관계(간선)가 얼마나 명확하고 논리적으로 타당한지를 나타내는 점수에서도 가장 높은 점수를 보여줌
4.3 Token/API Cost
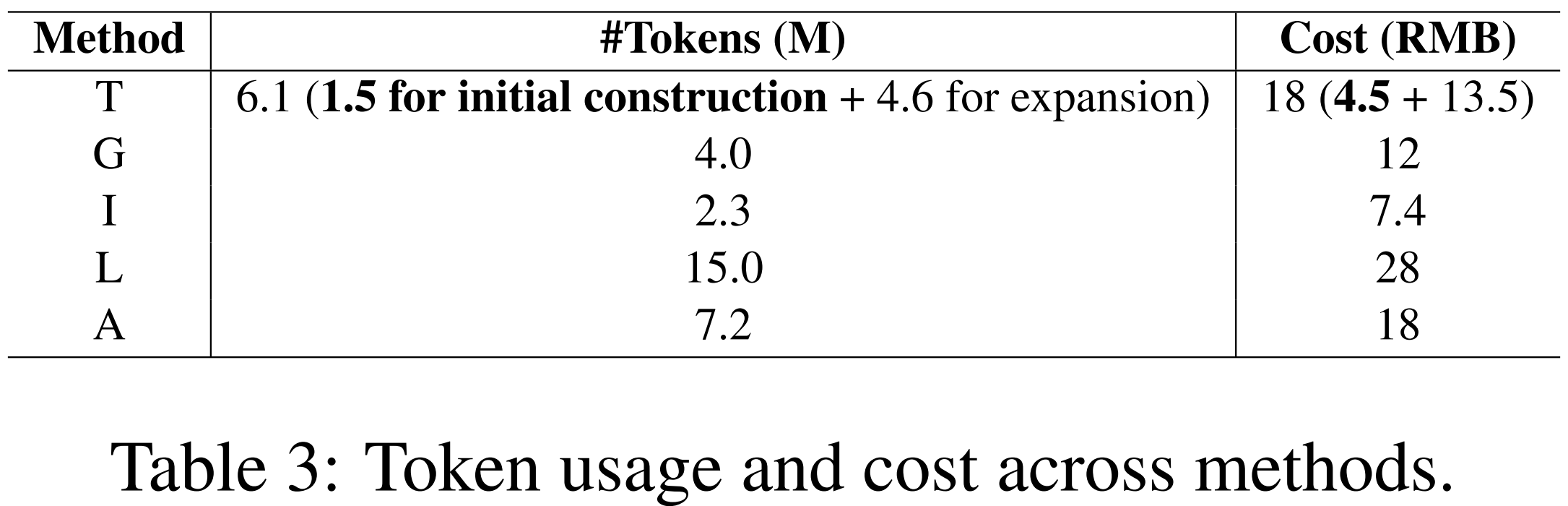
- DeepSeek-V3 API 사용
- 물리학(Physics) 도메인을 대상으로 비교
4.3.1 GraphRAG와의 비교
- GraphRAG (G)
- 계층 구조를 생성하기 위해 하향식 알고리즘(Hierarchical Leiden) 사용
- 방대한 양의 텍스트 요약을 수행하는 Bottom-up(상향식) 방식을 사용
- 토큰 소모가 많음
- Tree-KG (T)
- Iterative Expansion 단계는 필수 과정이 아니기 때문에 Initial Construction에 대해 비교
- Iterative Expansion 반복 횟수는 조절 가능
- 교과서의 기존 목차(TOC) 구조를 활용하는 Top-down(하향식) 방식을 취함
- 이 구조적 뼈대를 추출하는 과정에서는 토큰 비용이 발생하지 않기 때문에 GraphRAG에 비해 훨씬 효율적
4.3.2 Efficient Initial Construction
- Tree-KG의 초기 단계는 텍스트를 요약하는 작업만 수행
- 계층 구조를 처음부터 생성하는 GraphRAG에 비해 초기 구축 단계 비용이 훨씬 낮음
4.3.3 Selective Iterative Expansion
- Initial Construction: 4.5 RMB (저비용으로 기본 KG 생성)
- Iterative Expansion: 13.5 RMB (고품질을 위한 선택 사항)
- 사용자는 예산이나 필요에 따라 반복적 확장 단계를 생략하거나 조절
- 비용 관리가 매우 유연
4.3.4 성능-비용 균형 (Trade-off)
- iText2KG와 같이 비용이 더 적게 드는 모델도 존재
-
이들은 정보 추출의 품질이 낮다는 한계가 존재
- 한편, Tree-KG는 합리적인 자원 사용으로 강력한 성능을 달성
- 비용 대비 성능 측면에서 균형 잡힌 솔루션임
4.4 Ablation
- Tree-KG의 핵심 요소: Summerization, Contextual-based Convolution, Entity Deduplication, Edge Prediction
- 실제 성능 향상에 얼마나 기여하는지 검증
4.4.1 Summerization

- 성능 향상: 요약 단계를 거쳤을 때 ES는 9%, RS는 8% 향상
- 품질 정제: 관련 없거나 약한 연결고리를 줄어주어, 더 정확한 엔티티와 관계를 추출할 수 있게 도움
- 수치적 안정성: 추출되는 엔티티와 엣지의 개수가 훨씬 안정적으로 유지되어 시스템의 Robustness를 입증
4.4.2 Contextual-based Convolution
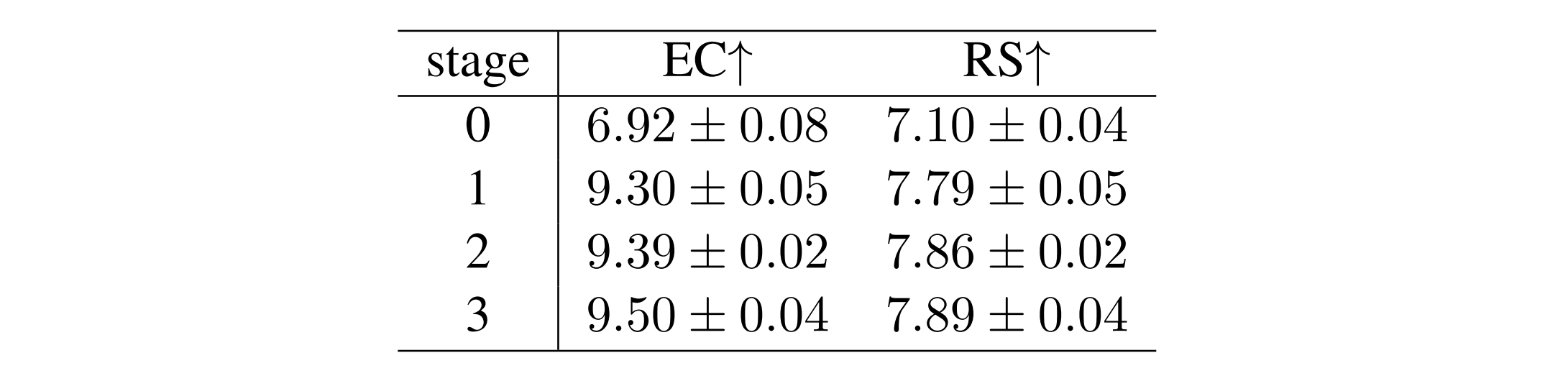
- 효율성 및 수렴성
- 단 1회의 합성곱 만으로도 EC는 34%, 관계 강도는 10% 개선
- 2회 이상 수행할 경우 성능 향상은 1% 미만에 불과하지만 토큰 사용량은 급격히 증가
- 따라서 1회만 수행하는 것이 가장 경제적
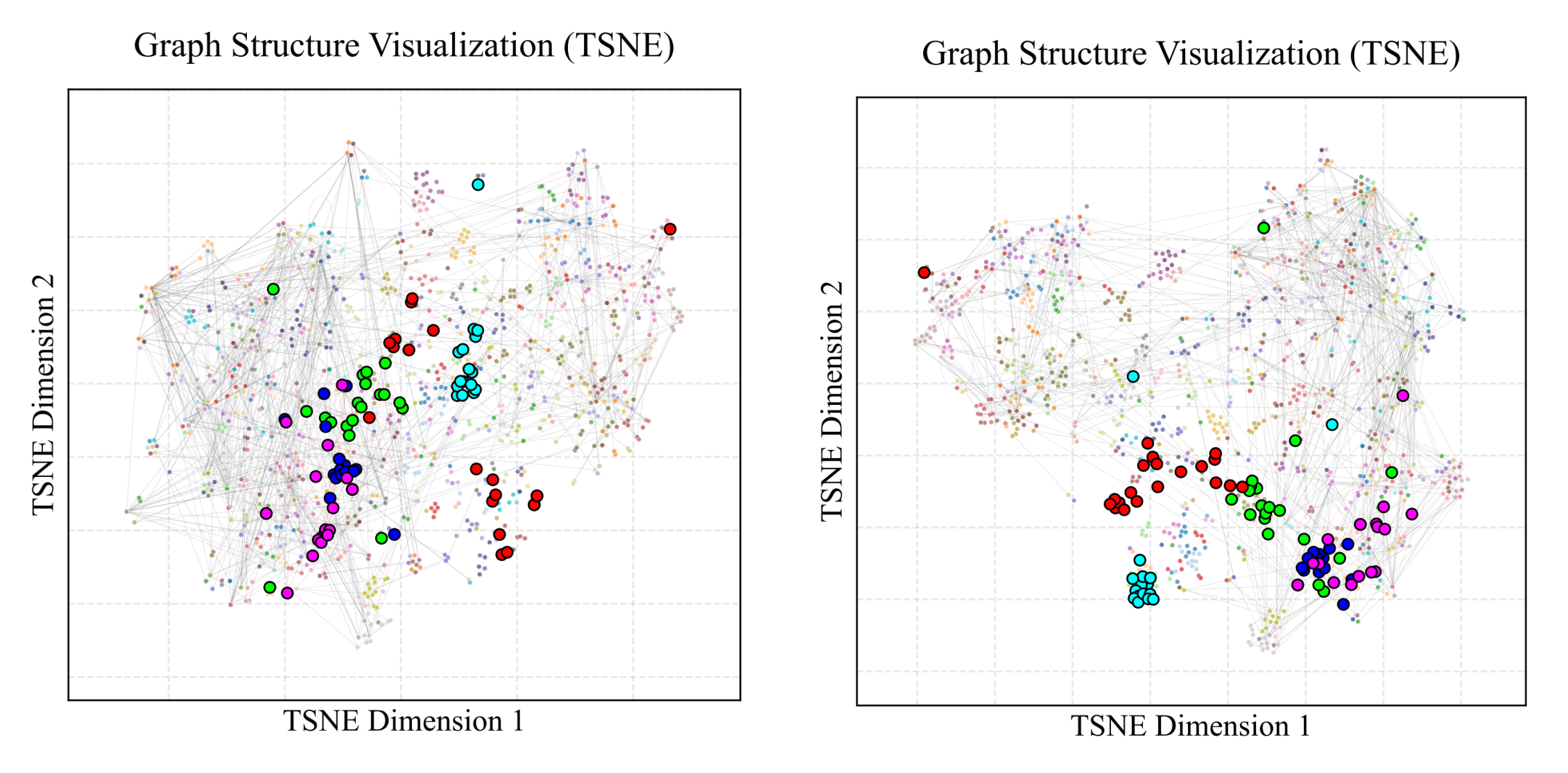
- 구조적 정렬 (t-SNE 시각화)
- Before Convolution: 같은 단원 소속이어도 텍스트 설명이 특징에 따라 임베딩이 흩어져 있음
- After Convolution: 같은 단원에 속한 엔티티들이 서로 군집을 이루는 현상이 발생
- 이는 텍스트 설명이 그래프의 구조와 일치하도록 정렬되었음을 의미하며
- 이는 나중에 중복 엔티티를 제거(Entity Deduplication, dedup)할 때 매우 유리하게 작용
4.4.3 Entity Deduplication
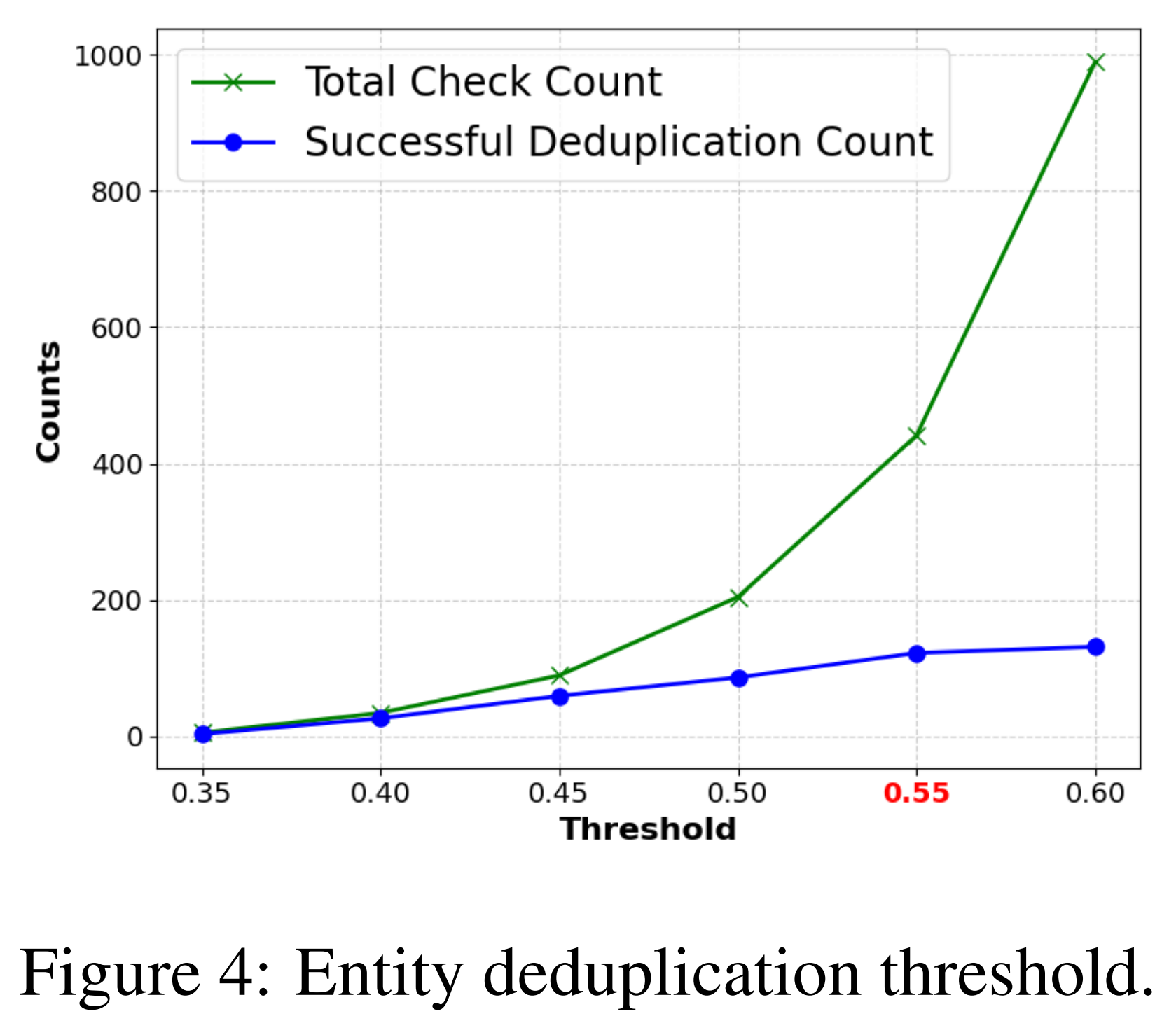
- 엔티티 중복 제거(dedup) 과정에서 가장 효율적인 임계값($threshold_{dedup}$)
- 임계값 증가에 따른 경향
- 임계값이 높아질수록 LLM이 확인해야 하는 전체 확인 횟수와 실제로 병합에 성공한 중복 제거 횟수가 모두 증가
- 비효율 구간(0.55 $0.55 \rightarrow 0.6$)
- 성공 횟수: 7% 증가
- 체크 횟수: 124% 폭증
- 임계값 증가에 따른 경향
4.4.4 Edge Prediction
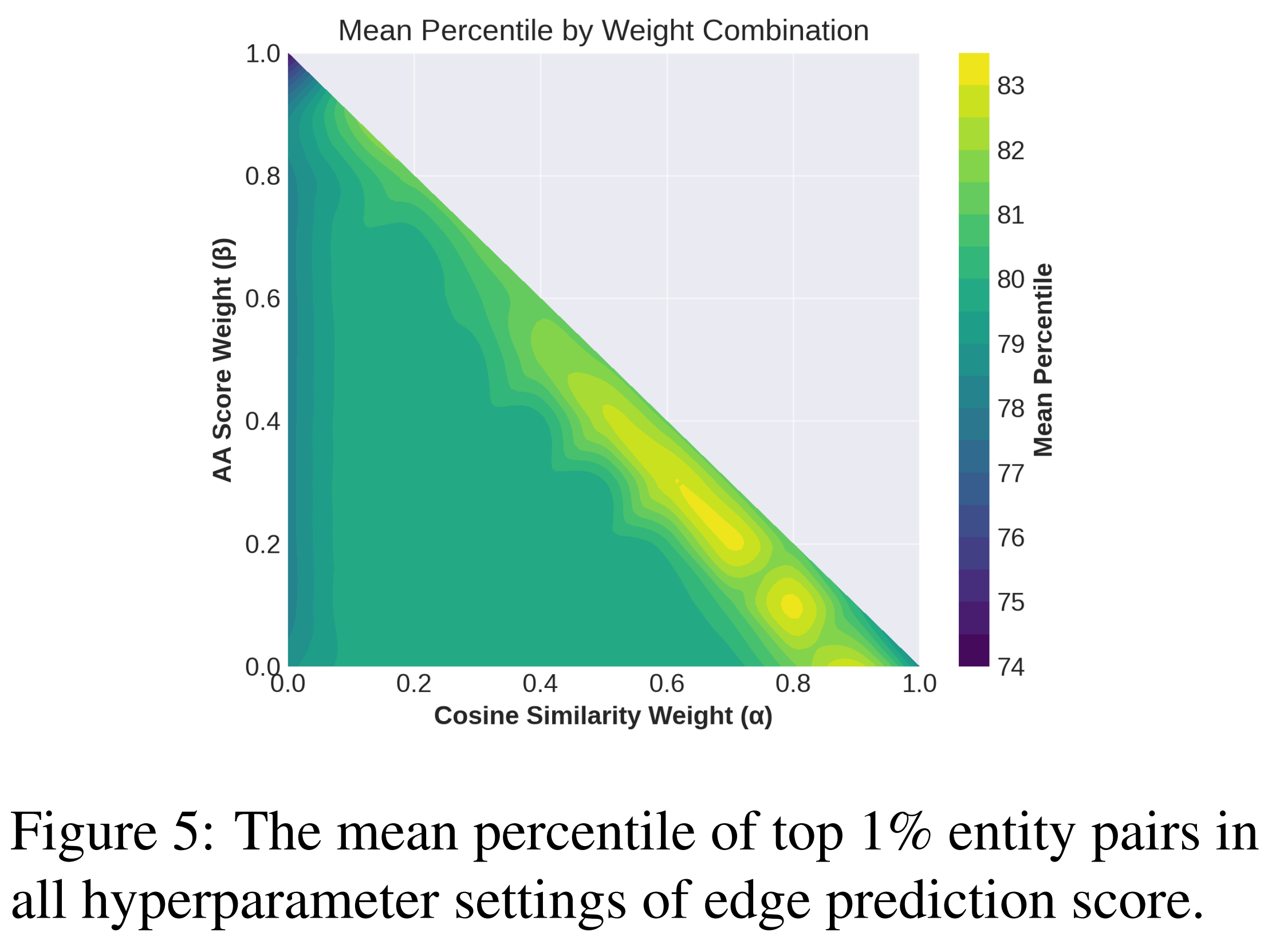
- 가중치의 의미와 설정 원칙
- $\alpha$: 의미적 관련성 (cosine similarity)
- $\beta$: 구조적 유사성 (Adamic-Adar Score, AA)
- $\gamma$: 계층적 근접성 (Common Ancestors, CA)
- 코사인 유사도가 가장 중요한 단서를 제공하고 그 다음으로 AA, 마지막으로 CA라 판단
- 따라서, 중요도 설정을 $\alpha > \beta > \gamma$ 순으로 설정
- 기존 설정: $\alpha = 0.6, \beta = 0.3, \gamma = 0.1$
- 실험 설계 및 평가 방식
- 조합 테스트: 세 가중치의 합이 1이 되는 모든 조합(0.1 단위, 총 66개)을 테스트
- 대상: 약 336,000개의 후보 엔티티 쌍에 대해 점수를 계산하고 순위를 매김
- 지표: 상위 1%(약 3,000 쌍)를 추출하여 이들이 각 지표에서 얼마나 높은 백분위에 위치하는지 평균을 계산
- 분석 결과
- 기존 설정
- $\alpha = 0.6, \beta = 0.3, \gamma = 0.1$ 조합에서 82.16%의 높은 평균 백분위 달성
- 실험 결과
- $\alpha = 0.8, \beta = 0.1, \gamma = 0.1$ 일 때 83.14%로 더 좋은 성능을 달성
- 결론
- 의미적 유사성($\alpha$)에 더 높은 가중치를 부여할수록 예측 성능이 향상된다는 것을 확인
- 즉, 텍스트가 가진 의미 자체가 관계를 예측하는 데 가장 결정적인 단서가 된다는 의미
- 기존 설정
5. Conclusion & Limitations
5-1. Conclusion
- 핵심 방법론
- 목차 등의 문서의 구조적 단서와 최신 LLM 기술 등을 결합
- 이를 통해 명시적인 트리 구조의 그래프를 먼저 구축하고 (Initial Construction, Construction of Skeleton)
- 이후 반복적인 확장(Iterative Expansion)을 통해 숨겨진 관계들을 효과적으로 찾아냄
- 성능 개선
- F1 Score
- 경쟁 모델 대비 일관되게 우수한 성능을 보임
- 2위 모델 대비 12~16% 더 높은 점수를 기록
- 정보 추출 능력
- 교과서 텍스트 기반(Text-Annotated) 데이터셋에서 0.81의 F1 Score를 달성
- 원본 텍스트에서 고품질 정보를 추출하는 능력을 입증
- F1 Score
- 구조적 정렬 및 효율성
- Tree-KG는 단순히 정보를 뽑는 것이 아닌 지식의 구조적 정렬 능력이 우수
- 토큰 사용량을 줄여 비용 효율적
- 자원 상황에 따라 유연하게 KG를 생성할 수 있는 모델
5-2. Limitations
- 현재 한계점
- 텍스트에 내재된 지식에 의존하여 그래프 생성
- 추론과 같은 다운스트림 작업을 수행할 때 기대만큼 성능이 나오지 않을 수 있음
- 즉, 그래프를 잘 만들기는 하지만, 그 그래프를 통해 복잡한 문제를 해결하는 것에는 아직 최적화되지 않음
- 향후 계획
- Task-specific한 작업을 수행할 수 있는 KG 구축 모델 제안 필요


댓글남기기