Juyeong Shin

KHU CSE 19
KHU DKE Lab.

8 분 소요

SeRF: Segment Graph for Range-Filtering Approximate Nearest Neighbor Search

About Paper

  • 제목: SeRF: Segment Graph for Range-Filtering Approximate Nearest Neighbor Search
  • 저널: ACM Manag. Data, Vol. 2, No. 1 (SIGMOD, Special Interest Group on Management of Data), Article 69. Feb 2024.
  • 저자: Chaoji Zuo, Miao Qiao, Wenchao Zhou, Feifei Li, Dong Deng

Introduction

ANN Search가 사용되는 분야

  • image, document, graph와 같은 실세계 데이터를 고차원 벡터로 임베딩하는 기술이 계속 발전하고 있음
  • 한편, 이러한 데이터는 timestamps, prices, quantities와 같은 structured data와 함께 연관되어 사용되곤 했음
    • 예시 1: 상품 탐색
      • 200달러 미만의 주어진 이미지와 비슷한 상품 탐색
    • 예시 2: 자동차 탐색
      • 도로 위 카메라는 주어진 이미지를 임베딩하여 벡터 생성
      • 생성된 벡터는 database timestamp에 저장 및 탐색
      • 번호판 없이, (time, space, image) 정보로 차량 특정
  • 그러나, 기존 RDBMS 기반 Filtering과 벡터 탐색을 동시에 수행하는 것은 여전히 데이터공학에서 도전적인 과제
    • 해당 문제 해결을 위한 다양한 질의 최적화 기법, 인덱싱 기법이 연구 중에 있음
    • 아직 많이 미흡한 상황..
    • 한번 떠올려보자. 이미지 검색과 동시에 다양한 필터링 조건을 붙여본 경험이 있던가?
  • 위 설명과 같이, 조건을 붙여 벡터를 탐색하는 기법을 RFANNS(Range-Filtering Approximate Nearest Neighbor Search)라 칭함
  • Range-Filtering ANNS(Approximate Nearest Neighbor Search)는 query range(질의 범위)와 query vector(질의 벡터)로 구성됨
    • 도전적인 과제인 이유는 생각보다 단순하다
    • 전체 벡터에 대한 인덱스는 존재하나, 필터링 된 벡터에 대한 인덱스는 없기 때문
  • 한편, 기존 range-filtering ANNS는 크게 2가지로 분류가 가능하다
    • ANNS-first (vectorDB-first)
      • ANNS-first는 주어진 query range에 부합할 때까지 ANN Search 수행
      • 주어진 query range에 부합하는 vector들을 반환
      • query range가 작은 경우, 조건에 부합하는 vector를 지속적으로 탐색하므로 수행 속도가 느리다
    • range-first (RDBMS-first)
      • 주어진 range에 따른 structured database에서 우선 탐색
      • structured database에서 필터링된 레코드에 대한 vector index가 구축되어 있지 않아 filtering 된 vector들은 naive한 탐색을 수행
      • 특히, range-first는 query range가 클 때, 비효율적
    • 주어진 상황에 어떤 전략을 취해야 할지에 대한 연구는 아래 논문을 참고하자

HNSW(Hierarchical Navigable Small World)

  1. Paper
    • Yu. A. Malkov, D. A. Yashunin. “Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World”. IEEE Transactions on pattern analysis and machine intelligence. 2018.
    • http://arxiv.org/pdf/1603.09320
  2. My Paper Review

Proposing Solution: Segment Graph

  • Half-bounded Range-Filtering ANNS Query: Segment Graph
    • Half-bounded: 주어진 set of vectors를 2개의 subset으로 분할
    • attribute에 따라 n개의 half-bounded hnsw index 생성 가능
    • 분할된 데이터를 통해 n개의 HNSW index 구축
    • 구축된 n개의 HNSW index를 무손실 압축하여 Segment Graph 구축
  • General Range-Filtering ANNS Query: 2D Segment Graph
    • N개의 Segment Graph를 통해 2D Segment Graph 구축

Preliminary

Segment

Segment의 사전적 의미

  • 명사: 부분, 단편, 분절(分節), 구분, 마디(division, section), 계층
  • 동사 전문 용어: (여러 부분으로)나누다, 분할하다

컴퓨터 공학에서 Segment

  • 컴퓨터 공학에서 Segment의 의미도 동일하다.
  • OS에서 Segmentation은 메모리 공간을 프로세스 단위로 나누어 관리하는 기법을 말하고
  • CV에서 Image Segmentation는 이미지에서 특정 개체를 추출(구분, 분할)하는 방법을 말한다
  • 또한, 자료구조에서 Segment Tree는 부분 질의에 대한 집계 결과들을 트리 형태로 관리하는 것을 말한다
    • 결론적인 기능 자체는 범위 질의에 대한 최대, 최소, 합, 곱 연산 결과를 미리 연산하면서 효율적인 접근이 가능한 형태의 트리로 관리하는 것이다

Prefix Sum

  • Segment Tree에 대해 살펴보기 전, Prefix Sum 부터 살펴보자.
  • 2번 idx에서부터 4번 idx까지의 부분합을 구한다고 하자
  • array에 값만 저장된 경우, 2번째 item, 3번째 item, 4번째 item을 모두 더하면 총 3번의 덧셈 연산이 필요
    • Time Complexity: $T(j - i + 1)$
  • item이 삽입될 때마다 누적합을 연산해두면 (4번째 누적합) - (1번째 누적합)으로 연산이 가능
    • Time complexity: $T(1)$

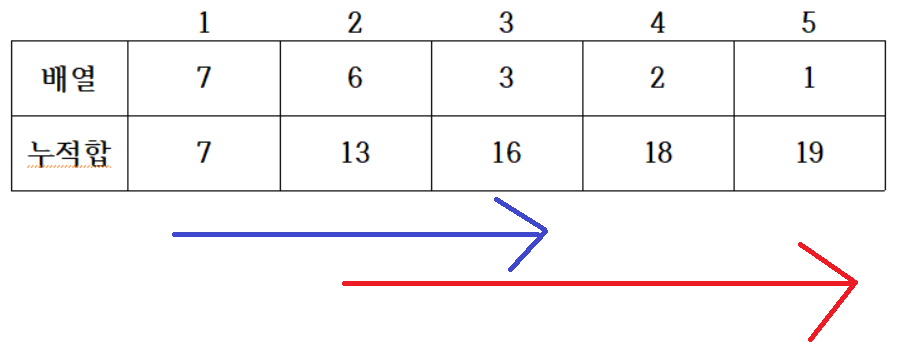
prefix_sum

  • 한편, 이러한 누적합은 update 연산 수행시, 시간복잡도가 증가한다는 단점을 가짐
    • 배열만 있는 경우: $O(1)$
    • 누적합 연산: $O(N)$

Segment Tree

  • Segment Tree에 대해 잠깐 짚어보고 넘어가자. 이번 포스팅에 꼭 필요한 지식은 아니나 아이디어 자체는 비슷하다고 생각한다
  • 길이가 1000인 array에서 10~100번 idx의 부분합을 구하려면 결국 해당 범위만큼의 복잡도가 따른다
    • 시작 범위를 $i$, 마지막 범위를 $j$라 하면, 시간복잡도는 $T(j-i+1)$ 이다
  • 한편, 아래와 같은 Segment Tree의 형태로 합 연산을 미리 저장해두면 $O(\log N)$ 의 복잡도를 보장해준다
  • 원하는 범위를 적절하게 포함하고 있는 노드 하나를 선택한 후 해당되지 않는 일부 범위를 빼거나 해당되는 일부 범위를 더하는 방식이다

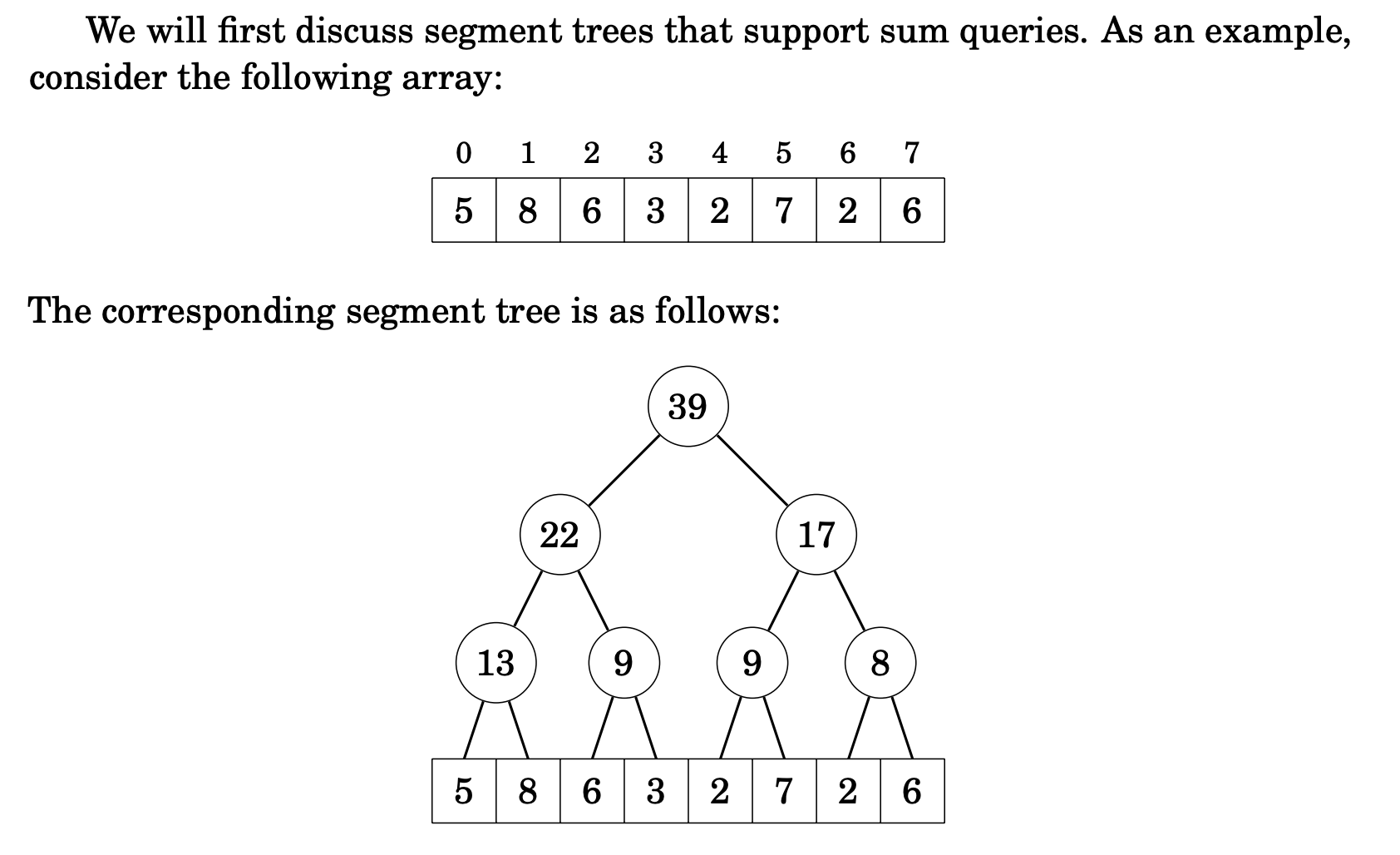
seg_tree

Range-Filtering

  • 특정 애트리뷰트에 조건을 달거나, 범위를 지정하여 필터링 한 후 다른 애트리뷰트를 다시 탐색하는 것
  • 질의최적화를 설명하라 할 때, 흔히 등장하는 예시이기도 하다(Column Oriented Database)
    • 경기도의 모든 인구(1400만)를 관리하는 테이블이 있다

    • 해당 테이블에서 14세 미만(160만)의 모든 남성(700만)을 찾고싶다

    • 이때, 14세 미만의 인구를 찾은 뒤 남성을 찾는게 빠를까

    • 아니면 남성을 찾은 뒤 그 중에서 14세 미만의 사람을 찾는게 빠를까

    • 전자는 1400만명 중에서 160만명을 찾고 160만명 중에서 80만명을 찾는다
      • 순차탐색을 진행한다 하였을 때, 1400만개의 레코드를 조회한 후 160만개의 레코드를 조회하니 총 1560만번의 조회가 발생했다
    • 후자는 1400만명 중에서 700만명을 찾고 700만명 중에서 80만명을 찾는다
      • 순차탐색을 진행한다 하였을 때, 1400만개의 레코드를 조회한 후 700만개의 레코드를 조회하니 총 2100만번의 조회가 발생했다
    • 결론적으로 전자가 더 효율적인 접근이다!
  • 얘기가 산으로 간 느낌이 강하지만, 결론적으로 위와 같은 상황을 Range-Filtering이라 한다
  • kNN(k-Nearest Neighbors, 최근접 이웃 알고리즘)의 일종이다
  • 인공지능 모델로 임베딩된 벡터들을 다시 조회하고 싶을 때 사용하는 알고리즘이다
    • 비슷한 이미지 찾기, 비슷한 음성 찾기, …
  • 그러나, 기존 kNN의 경우 임베딩 벡터의 차원이 증가함에 따라 복잡도가 선형적으로 증가하여 바로 적용하기 무리인 부분이 존재한다(k-D Tree, Ball Tree)
  • 이에 새로 등장하는 대안이 ANNS이고 대표적인 알고리즘으로는 HNSW, Vamana, NSG, ANNOY, IVFPQ 등이 존재한다
    • Graph-Based ANNS
      • HNSW, Vamana, NSG
      • 자료구조 상에서의 dimension에 따른 penalty를 회피하는 방식
      • Greedy Search를 주로 사용(Approximate Navigating)
      • 이웃 간 거리를 비교하여 당장의 최선의 후보를 선택하는 방식
      • 거리 비교 시에는 dimension에 의존적이나, k-D트리와 같이 구조 자체가 dimension에 의존적이지 않다
    • Tree-Based ANNS
      • ANNOY
      • 트리를 계층적으로 생성하여 비교군의 개수 자체를 줄이는 방식
    • IVFPQ(Inverted File index & Product Quantization)
      • PQ를 통해 클러스터를 나눈 후, 해당 클러스터 내에서 최근접 이웃을 탐색
      • Qunatized Vector를 통해 적절한 Voronoi Cell(클러스터)에 접근, 해당 클러스터 내에서 최근접 이웃을 탐색
      • Qunatized Vector는 원본 벡터의 차원을 손실 압축한 것
      • 즉, PQ는 dimension 자체를 낮춘다
  • kNN과 달리, ANNS 알고리즘은 정확한 k개의 최근접 이웃을 반환하지 않지만, 고차원 벡터 데이터를 보다 효율적으로 접근할 수 있게 한다

Segment Graph

  • Segment Tree는 범위 질의의 합 연산(혹은 곱, 최대, 최소)와 같은 연산에 사용
  • 한편, Segment Graph는 범위 질의에 해당하는 $k$개의 Nearest Neighbor를 반환하는 것이 목표
  • 이러한 목적을 달성하기 위한 Segment Graph를 어떻게 생성하고 질의를 처리할 것인가?
    • 논문에서는 누적합과 같은 원리로 1개의 노드만 포함한 Indexing Graph, 2개의 노드를 포함한 Indexing Graph, …, n(전체)개의 노드를 포함한 Indexing Graph를 Straight-Forward Idea로 우선 제시
    • 각 단계(1개 노드, 2개 노드, …, n개 노드) 별 그래프의 노드, 엣지 변화량만을 기록해 압축하여 최종 Segment Graph 저장
    • 위와 같은 방식은 1에서 임의의 i번재 범위까지의 질의를 처리
    • 한편, 2D Segment Graph를 제안하여 임의의 i에서부터 j까지의 범위 질의를 처리하는 기법 제안

Notations

  • d-dimensional space: $\mathbb{R}^d$
  • distance metric(e.g. euclidean distance, cosine distance): $\delta$
  • set of n points: $D, n > 0$
  • Nearest Neighbor Search
    • given query point: $q \in \mathbb{R}^d$
    • k-nearest neighbor search: $kNN_{\delta}(q, D)$
      • e.g., 1-nearest neighbor search: $1NN_{\delta}(q, D)$
    • set of k-nearest neighbor search results: $S \subseteq D$

Problem Definitions with Attribute Filtering

Problem 1. Filtering with attributes

  • Let $D$ with vector data points: $v, v \in D$
  • Let $A$ be an attributes with specific domain $Dom(A)$
    • $Dom(A)$ has a total order
    • total order(전순서 집합): 정렬 가능한 집합, 아래와 같은 성질을 가진다.
      • 비반사성(irreflexibe): $a \leq a$ 이다.
      • 전이성(transitive): 만약 $a \leq b$ 이고 $b \leq c$ 이면 $a \leq c$ 이다.
      • 반대칭성(antisymetric): 만약 $a \leq b$ 이고 $b \leq a$ 라면 $a = b$ 이다.
      • 연결성(connected): $a \leq b$ 이거나 $b \leq a$ 이다.
    • total order를 가진다는 것은 정렬 가능하다는 것이지, 정렬이 되어있다는 것이 아니다.
  • The attribute associated with $v$: $v[A]$
  • Let $I_A$ be any interval on $Dom(A)$
    • i.e., $D[I_A] = {v \in D \mid v[A] \in I_A }$
  • To simplify search, sort the data points in $D$ in ascending order of ther $A$
    • The attribute associated with $v$: $v[A]$
    • key: attribute, $Dom(A)$
    • value: vector, $v$

  • i.e., for any $v_i, v_j \in D$, $i < j$ implies $v_i[A] \leq v_j[A]$

  • 이에 따라, key(i.e., $a \in Dom(A)$)가 주어지는 경우, $D$에서 해당 해당 attribute에 대응하는 벡터를 찾는 복잡도는 $O(log(n))$ 이다

  • 말이 되게 복잡했지만, attribute를 정렬하여 이분 탐색을 통해 주어진 도메인의 attribute에 해당하는 벡터를 탐색하는 복잡도는 $O(log(n))$ 이라는 것이다.
    • Key를 Sorted List 형식으로 관리하는 Sorted Map을 생각하면 될 것 같다.
    • key: attribute with specific domain, i.e., $Dom(A)$
    • value: vector, i.e., $v \in D$
    • 해당 key를 찾는 검색 시간 복잡도는 $O(log(n))$
    • 해당 value로 매핑되는 복잡도는 $O(1)$

Definition

  • Let $D$ with vector data points: $v, v \in D$
    • size of vector set: $n$. i.e., $\lvert D \rvert = n$
  • The key of point $v_i \in D$ is $i$
  • For each $i \in [n]$ , Range-Filtered Query Result: $Q = (q, [i, j], k)$
    • $i, j \in [n]$ $and$ $0 < k \leq j-i+1$
    • $Q = kNN(q, d_{i, j})$

Example

rfanns_problem_definition

  • Consider the set of $n = 20$ points $D = {v_1, …, v_{20}}$
  • The range-filtering nearest neighbor search query $Q = (q, [4, 13], 1)$
    • query point: $q$
    • query range(attribute range): $[4, 13]$
    • $k$ nearest neighbor: $1$
  • Distance to given query point: $\delta(v_i, q)$
  • The query $Q$ returns $1NN(q, D_{4, 13}) = {v_{11}}$
    • Though $v_{18}$ and $v_{15}$ are closer to the query point q than $v_{11}$,
    • their keys $18$ and $15$ are not within the query range $[4, 13]$
  • 보면 알겠지만, key에 대해서 정렬을 해놓으니 벡터들의 순서가 엉망진창이다.
  • 반대로, 어떻게든 벡터들을 정렬시켜 효율적인 탐색을 가능하게끔 만든다고 하면, key에 대한 순서가 엉망진창일 것이다.
  • 위 예시는 key에 대한 탐색 후 벡터를 탐색하는 range-first에 대한 설명으로도 볼 수 있다.
  • 처음 말했듯이, key, i.e., attribute에 대한 탐색은 $O(log(n))$ 을 보장하나, value, i.e., vector에 대한 탐색은 해당 범위 내에서 완전탐색을 수행해야 한다.

Problem 3. RFANNS Recall Score

  • RFANNS: Range Filtering Approximate Nearest Neighbor Search
  • Range-Filtering Approximate Nearest Neighbor Search Query: $Q = (q, [i, j], k)$
  • $Q$ aims at reporting $kANN(q, D_{i, j})$
    • range: $[i, j]$
    • $D = D_{1, n}$
  • Optimized Recall per 1 Query: ${\frac{\mid kANN(q, D_{i, j}) \cap kNN(q, D_{i, j}) \mid}{k}}$
    • kANN(k Approximate Nearest Neighbors)에서 반환된 $k$개의 이웃 중에서, kNN(k Nearest Neighbors)에서 반환한 실제 최근접 이웃의 비율

HNSW Graphs for Half-bounded Query Ranges

Segment Graph

HNSW Graphs for Arbitrary Query Ranges

2D Segment Graph

Experiment

Conclusion

References

댓글남기기

참고

멀티 쓰레딩 환경에서 캐시 미스에 대해

4 분 소요

멀티 쓰레딩 환경에서 캐시 미스에 대해 CPU 캐시의 구조 이번 포스팅에 앞서, numpy가 더 빠른 이유 - 캐시메모리 입장에서를 먼저 보고 오길 권장한다. CPU 캐시 메모리에 대한 대략적인 이해 후 이번 포스팅을 보는 것이 훨씬 이해에 도움이 될 것이다.

Randomized Quick Sort와 느낀 점

1 분 소요

Randomized Quick Sort와 느낀 점 Quick Sort Quick Sort는 분할정복 알고리즘(Divide & Conquer)으로서, pivot을 잡고 partiton 함수로 pivot보다 작은 item들은 왼쪽에, pivot보다 큰 item들은 오른쪽에...

BST(Binary Search Tree)와 KD트리 그리고 B트리와 R트리

11 분 소요

BST(Binary Search Tree)와 KD트리 그리고 B트리와 R트리 트리를 이용한 인덱싱 기법들.. 근데 이제, 다차원을 곁들인 자료구조를 공부한 적이 있다면 BST(Binary Search Tree, 이진탐색트리)도 배웠을 것이다.